题目内容
【题目】已知二次函数y=-x2-2x+3.
(1)求抛物线顶点M的坐标;
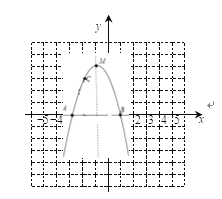
(2)设抛物线与x轴交于A,B两点,与y轴交于C点,求A,B,C的坐标(点A在点B的左侧),并画出函数的图象;
(3)根据图象,写出当![]() <
<![]() 时,
时, ![]() 的取值范围.
的取值范围.

【答案】(1)顶点![]() 的坐标为(-1,4);(2)略;(3)
的坐标为(-1,4);(2)略;(3)![]() < -3或
< -3或![]() >1
>1
【解析】试题分析:(1)先配方得到顶点式: ![]() ,则可写出顶点坐标,
,则可写出顶点坐标,
(2)把x=0代入解析式可求得对应函数值,即可求得抛物线与y轴交点C的坐标,把y=0代入解析式求得对应的自变量,即可求得抛物线与x轴的交点A,B的坐标,然后描点画图,
(3) 观察二次函数图象![]() <
<![]() 的部分所对应的自变量x的取值范围,可得
的部分所对应的自变量x的取值范围,可得![]() < -3或
< -3或![]() >1.
>1.
试题解析:(1)y=-x2-2x+3=-(x+1)2+4,
∴ 抛物线顶点M的坐标为(-1,4),
(2) 把x=0代入![]() 可得y=3,所以点C(0,3), 把y=0代入
可得y=3,所以点C(0,3), 把y=0代入![]() ,解得:
,解得: ![]() -3
-3![]() 1,所以点A(-3,0),B(1,0),
1,所以点A(-3,0),B(1,0),
(3)由图象可知, ![]() < -3或
< -3或![]() >1.
>1.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

