题目内容
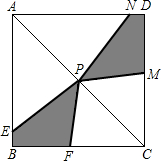 (2013•杭州)如图,已知正方形ABCD的边长为4,对称中心为点P,点F为BC边上一个动点,点E在AB边上,且满足条件∠EPF=45°,图中两块阴影部分图形关于直线AC成轴对称,设它们的面积和为S1.
(2013•杭州)如图,已知正方形ABCD的边长为4,对称中心为点P,点F为BC边上一个动点,点E在AB边上,且满足条件∠EPF=45°,图中两块阴影部分图形关于直线AC成轴对称,设它们的面积和为S1.(1)求证:∠APE=∠CFP;
(2)设四边形CMPF的面积为S2,CF=x,y=
| S1 | S2 |
①求y关于x的函数解析式和自变量x的取值范围,并求出y的最大值;
②当图中两块阴影部分图形关于点P成中心对称时,求y的值.
分析:(1)利用正方形与三角形的相关角之间的关系可以证明结论;
(2)本问关键是求出y与x之间的函数解析式.
①首先分别用x表示出S1与S2,然后计算出y与x的函数解析式.这是一个二次函数,求出其最大值;
②注意中心对称、轴对称的几何性质.
(2)本问关键是求出y与x之间的函数解析式.
①首先分别用x表示出S1与S2,然后计算出y与x的函数解析式.这是一个二次函数,求出其最大值;
②注意中心对称、轴对称的几何性质.
解答:(1)证明:∵∠EPF=45°,
∴∠APE+∠FPC=180°-45°=135°;
而在△PFC中,由于PC为正方形ABCD的对角线,则∠PCF=45°,
则∠CFP+∠FPC=180°-45°=135°,
∴∠APE=∠CFP.
(2)解:①∵∠APE=∠CFP,且∠FCP=∠PAE=45°,
∴△APE∽△CFP,则
=
.
而在正方形ABCD中,AC为对角线,则AC=
AB=4
,
又∵P为对称中心,则AP=CP=2
,
∴AE=
=
=
.
如图,过点P作PH⊥AB于点H,PG⊥BC于点G,
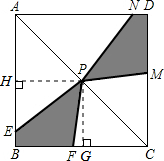
P为AC中点,则PH∥BC,且PH=
BC=2,同理PG=2.
S△APE=
PH•AE=
×2×
=
,
∵阴影部分关于直线AC轴对称,
∴△APE与△APN也关于直线AC对称,
则S四边形AEPN=2S△APE=
;
而S2=2S△PFC=2×
=2x,
∴S1=S正方形ABCD-S四边形AEPN-S2=16-
-2x,
∴y=
=
=-
+
-1.
∵E在AB上运动,F在BC上运动,且∠EPF=45°,
∴2≤x≤4.
令
=a,则y=-8a2+8a-1,当a=-
=
,即x=2时,y取得最大值.
而x=2在x的取值范围内,代入x=2,则y最大=4-2-1=1.
∴y关于x的函数解析式为:y=-
+
-1(2≤x≤4),y的最大值为1.
②图中两块阴影部分图形关于点P成中心对称,
而此两块图形也关于直线AC成轴对称,则阴影部分图形自身关于直线BD对称,
则EB=BF,即AE=FC,
∴
=x,解得x=2
,
代入x=2
,得y=2
-2.
∴∠APE+∠FPC=180°-45°=135°;
而在△PFC中,由于PC为正方形ABCD的对角线,则∠PCF=45°,
则∠CFP+∠FPC=180°-45°=135°,
∴∠APE=∠CFP.
(2)解:①∵∠APE=∠CFP,且∠FCP=∠PAE=45°,
∴△APE∽△CFP,则
| AP |
| CF |
| AE |
| PC |
而在正方形ABCD中,AC为对角线,则AC=
| 2 |
| 2 |
又∵P为对称中心,则AP=CP=2
| 2 |
∴AE=
| AP•PC |
| CF |
2
| ||||
| x |
| 8 |
| x |
如图,过点P作PH⊥AB于点H,PG⊥BC于点G,

P为AC中点,则PH∥BC,且PH=
| 1 |
| 2 |
S△APE=
| 1 |
| 2 |
| 1 |
| 2 |
| 8 |
| x |
| 8 |
| x |
∵阴影部分关于直线AC轴对称,
∴△APE与△APN也关于直线AC对称,
则S四边形AEPN=2S△APE=
| 16 |
| x |
而S2=2S△PFC=2×
| PG•CF |
| 2 |
∴S1=S正方形ABCD-S四边形AEPN-S2=16-
| 16 |
| x |
∴y=
| S1 |
| S2 |
16-
| ||
| 2x |
| 8 |
| x2 |
| 8 |
| x |
∵E在AB上运动,F在BC上运动,且∠EPF=45°,
∴2≤x≤4.
令
| 1 |
| x |
| 8 |
| -2×8 |
| 1 |
| 2 |
而x=2在x的取值范围内,代入x=2,则y最大=4-2-1=1.
∴y关于x的函数解析式为:y=-
| 8 |
| x2 |
| 8 |
| x |
②图中两块阴影部分图形关于点P成中心对称,
而此两块图形也关于直线AC成轴对称,则阴影部分图形自身关于直线BD对称,
则EB=BF,即AE=FC,
∴
| 8 |
| x |
| 2 |
代入x=2
| 2 |
| 2 |
点评:本题是代数几何综合题,考查了正方形的性质、相似三角形、二次函数的解析式与最值、几何变换(轴对称与中心对称)、图形面积的计算等知识点,涉及的考点较多,有一定的难度.本题重点与难点在于求出y与x的函数解析式,在计算几何图形面积时涉及大量的计算,需要细心计算避免出错.

练习册系列答案
相关题目
 (2013•杭州)如图,设k=
(2013•杭州)如图,设k=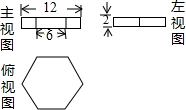 (2013•杭州)如图是某几何体的三视图,则该几何体的体积是( )
(2013•杭州)如图是某几何体的三视图,则该几何体的体积是( ) (2013•杭州)如图,四边形ABCD是矩形,用直尺和圆规作出∠A的平分线与BC边的垂直平分线的交点Q(不写作法,保留作图痕迹).连结QD,在新图形中,你发现了什么?请写出一条.
(2013•杭州)如图,四边形ABCD是矩形,用直尺和圆规作出∠A的平分线与BC边的垂直平分线的交点Q(不写作法,保留作图痕迹).连结QD,在新图形中,你发现了什么?请写出一条.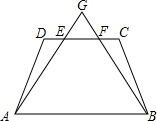 (2013•杭州)如图,在等腰梯形ABCD中,AB∥DC,线段AG,BG分别交CD于点E,F,DE=CF.
(2013•杭州)如图,在等腰梯形ABCD中,AB∥DC,线段AG,BG分别交CD于点E,F,DE=CF.