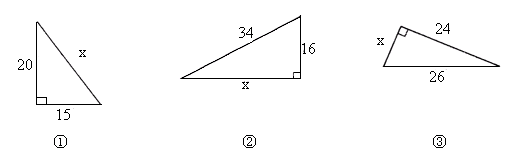题目内容
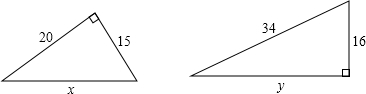
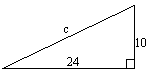
求下列直角三角形中未知边的长度.

解:①由勾股定理得:x2=202+152,
x=±25,
∵x表示边长,
∴x=25;
②由勾股定理得:y2=342-162,
y=±30,
∵y表示边长,
∴y=30.
分析:根据勾股定理:如果直角三角形的两条直角边长分别是a,b,斜边长为c,那么a2+b2=c2.代入数进行计算即可.
点评:此题主要考查了勾股定理,关键是熟练掌握勾股定理.直角三角形中的三边长可以利用勾股定理知二求一.
x=±25,
∵x表示边长,
∴x=25;
②由勾股定理得:y2=342-162,
y=±30,
∵y表示边长,
∴y=30.
分析:根据勾股定理:如果直角三角形的两条直角边长分别是a,b,斜边长为c,那么a2+b2=c2.代入数进行计算即可.
点评:此题主要考查了勾股定理,关键是熟练掌握勾股定理.直角三角形中的三边长可以利用勾股定理知二求一.

练习册系列答案
相关题目