题目内容
正比例函数y=kx（k≠0）的图象经过点（-1，2），并且点A（x1，y1），B（x2，y2）也在该正比例函数图象上，若x1-x2=3，则y1-y2的值为（ ）
分析：首先利用待定系数法求得k的值；然后将点A、B的坐标分别代入该函数解析式并分别求得y1、y2的值．
解答：解：∵正比例函数y=kx（k≠0）的图象经过点（-1，2），
∴2=-k，即k=-2，
∴该正比例函数的解析式是y=-2x．
又∵点A（x1，y1），B（x2，y2）也在该正比例函数图象上，
∴y1=-2x1，①
y2=-2x2，②
由①-②，得
y1-y2=-2（x1-x2）=-2×3=-6．
故选D．
∴2=-k，即k=-2，
∴该正比例函数的解析式是y=-2x．
又∵点A（x1，y1），B（x2，y2）也在该正比例函数图象上，
∴y1=-2x1，①
y2=-2x2，②
由①-②，得
y1-y2=-2（x1-x2）=-2×3=-6．
故选D．
点评：本题考查了一次函数图象上点的坐标特征：在这条直线上的各点的坐标一定适合这条直线的解析式．
练习册系列答案
相关题目
已知正比例函数y=kx的图象经过点P（-1，2），则k的值是（ ）
| A、2 | ||
B、
| ||
| C、-2 | ||
D、-
|
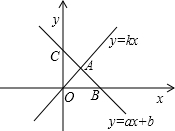正比例函数y=kx和一次函数y=ax+b的图象都经过A（1，2），且一次函数的图象交x轴于点B（3，0），交y轴于C点．