题目内容
老师出了如下的题:
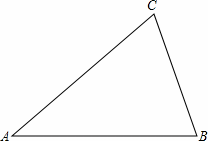
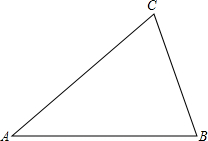
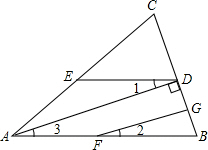
(1)首先,要求你按图1回答以下问题
①若∠DEC+∠ACB=180°,可以得到哪两条线段平行?
②在①的结论下,如果∠1=∠2,又能得到哪两条线段平行,请说明.
(1)①______∥______.
②______.
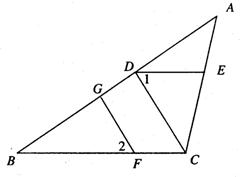
(2)接着,老师另画了一个图2
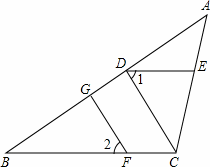
①要求你在图2中按下面的语言继续画图:(画图工具和方法不限)过A点画AD⊥BC于D,过D点画DE∥AB交AC于E,在线段AB上任取一点F,以F为顶点,FB为一边,画∠BFG=∠ADE,∠BFG的另一边FG与线段BC交于点G.
②请你按照①中画图时给出的条件,完整证明:FG⊥BC.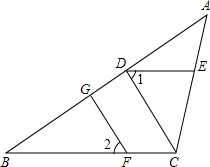
(1)首先,要求你按图1回答以下问题
①若∠DEC+∠ACB=180°,可以得到哪两条线段平行?
②在①的结论下,如果∠1=∠2,又能得到哪两条线段平行,请说明.
(1)①______∥______.
②______.
(2)接着,老师另画了一个图2
①要求你在图2中按下面的语言继续画图:(画图工具和方法不限)过A点画AD⊥BC于D,过D点画DE∥AB交AC于E,在线段AB上任取一点F,以F为顶点,FB为一边,画∠BFG=∠ADE,∠BFG的另一边FG与线段BC交于点G.

②请你按照①中画图时给出的条件,完整证明:FG⊥BC.

(1)①DE∥BC,
②可得DC∥FG,
说明:∵DE∥BC,∴∠1=∠3.
又∵∠1=∠2,
∴∠2=∠3,
∴DC∥FG.
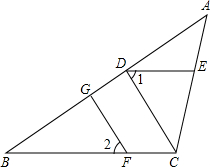
(2)证明:如下图所示:
∵DE∥AB,
∴∠1=∠3.
又∵∠1=∠2,
∴∠2=∠3,
∴AD∥FG.
∵AD⊥BC于D,
∴∠CDA=90°.
∵AD∥FG,
∴∠FGD=∠CDA=90°,
∴FG⊥BC.
②可得DC∥FG,
说明:∵DE∥BC,∴∠1=∠3.
又∵∠1=∠2,
∴∠2=∠3,
∴DC∥FG.

(2)证明:如下图所示:
∵DE∥AB,
∴∠1=∠3.
又∵∠1=∠2,
∴∠2=∠3,
∴AD∥FG.
∵AD⊥BC于D,
∴∠CDA=90°.
∵AD∥FG,
∴∠FGD=∠CDA=90°,
∴FG⊥BC.

练习册系列答案
相关题目
 26、老师出了如下的题:
26、老师出了如下的题:
 老师出了如下的题:
老师出了如下的题: