Question

（2011广西崇左，24，14分）（本小题满分14分）如图，在边长为8的正方形ABCD

中，点O为AD上一动点（4＜OA＜8），以O为圆心，OA的长为半径的圆交边CD于点M，连接OM，过点M作圆O的切线交边BC于点N.

（1）       求证：△ODM∽△MCN；

（2）       设DM=x，求OA的长（用含x的代数式表示）；

（3）       在点O运动的过程中，设△CMN的周长为p，试用含x的代数式表示p，你能发现怎样的结论？

 

Answer 1

（1）证明：∵MN为切线，∴OM⊥MN，

∴∠NMC=90°-∠OMD=∠DOM，

∴Rt△DOM∽Rt△CMN.

（2）设OA=y，Rt△ODM中，DM ²=OM ²- DO ²=OA ²- DO²,

即x²=y²-(8-y)²,解得OA=y =

（3）由（1）知△DOM ∽△CMN，相似比为，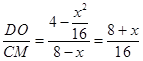

故p=.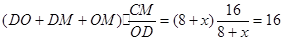

故p为定值16.

解析:略