题目内容
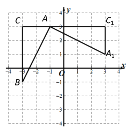
【题目】如图,在平面直角坐标系中,有一Rt△ABC,∠C=90°且A(-1,3)、B(-3,-1)、C(-3,3),已知△A1AC1是由△ABC旋转得到的.若点Q在x轴上,点P在直线AB上,要使以Q、P、A1、C1为顶点的四边形是平行四边形,满足条件的点Q的坐标为______.
【答案】(-1.5,0)或(-3.5,0)或(6.5,0)
【解析】
用待定系数法先求出直线AB的解析式,然后再根据A1 C1为平行四边形的边和平行四边形的对角线两种情况分别进行求解即可.
∵由图可知A(-1,3),B(-3,-1),
∴设直线AB的解析式为y=kx+b(k≠0),则
![]() ,解得
,解得![]() ,
,
∴直线AB的解析式为:y=2x+5;
∵点Q在x轴上,点P在直线AB上,以Q、P、A1、C1为顶点的四边形是平行四边形,
当A1C1为平行四边形的边时,
则PQ// A1 C1//y轴,PQ=A1 C1=2,
∵P点在直线y=2x+5上,
∴令y=2时,2x+5=2,解得x=-1.5,
令y=-2时,2x+5=-2,解得x=-3.5,
∴P(-1.5,2)或(-3.5,-2),
∴Q(-1.5,0)或(-3.5,0);
当A1C1为平行四边形的对角线时,
∵A1C1的中点坐标为(3,2),
∴P的纵坐标为4,
代入y=2x+5得,4=2x+5,
解得x=﹣0.5,
∴P(﹣0.5,4),
3-(-0.5)=3.5,3+3.5=6.5,
∴Q(6.5,0),
综上,Q点坐标为:(-1.5,0)或(-3.5,0)或(6.5,0),
故答案为:(-1.5,0)或(-3.5,0)或(6.5,0).

 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案【题目】目前![]() 节能灯在城市已基本普及,为面向乡镇市场,苏宁电器分店决定用76000元购进室内用、室外用节能灯,已知这两种类型的节能灯进价、售价如下:
节能灯在城市已基本普及,为面向乡镇市场,苏宁电器分店决定用76000元购进室内用、室外用节能灯,已知这两种类型的节能灯进价、售价如下:
价格 类型 | 进价(元/盏) | 售价(元/盏) |
室内用节能灯 | 40 | 58 |
室外用节能灯 | 50 | 70 |
(1)若该分店共购进节能灯1700盏,问购进的室内用、室外用节能灯各多少盏?
(2)若该分店将进货全部售完后获利要不少于32000元,问至少需要购进多少盏室内用节能灯?
(3)挂职锻炼的大学生村官王祥自酬了4650元在该分店购买这两种类型的节能灯若干盏,分发给村民使用,其中室内用节能灯盏数不少于室内用节能灯盏数的2倍,问王祥最多购买室外用节能灯多少盏?