题目内容
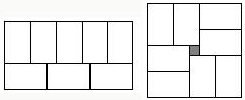
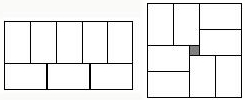这张师傅在铺地板时发现：用8个大小一样的长方形瓷砖恰好可以拼成一个大的长方形（如图），然后，他用这8块瓷砖七拼八凑，又拼出了一个正方形，中间还留下一个2cm×2cm的小正方形（阴影部分）．请你根据提供的信息，求出这些长方形的长和宽．
分析：仔细观察图形，发现本题中2个等量关系为：小长方形的长×3=小长方形的宽×5，（小长方形的长+小长方形的宽×2）2=小长方形的长×小长方形的宽×8+2×2．根据这两个等量关系可列出方程组．
解答：解：设这8个大小一样的小长方形的长为xcm，宽为ycm．
由题意，得
，
解得
．
答：这些长方形的长和宽分别为10cm，6cm．
由题意，得
|
解得
|
答：这些长方形的长和宽分别为10cm，6cm．
点评：解题关键是弄清题意，找到合适的等量关系，列出方程组．解决本题需仔细观察图形，发现大长方形的对边相等及正方形的面积=8个小长方形的面积+边长为2cm的小正方形的面积是关键．
练习册系列答案
精英口算卡系列答案
相关题目
张师傅在铺地板时发现，用8块大小一样的长方形瓷砖恰好可以拼成一个大的长方形，如图1．然后，他用这8块瓷砖又拼出一个正方形，如图2，中间恰好空出一个边长为1的小正方形（阴影部分），假设长方形的长y，宽为x，且y＞x．
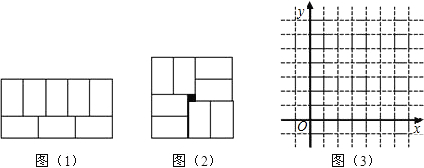
（1）请你求出图1中y与x的函数关系式；
（2）求出图2中y与x的函数关系式；
（3）在图3中作出两个函数的图象，写出交点坐标，并解释交点坐标的实际意义；
（4）根据以上讨论完成下表，观察x与y的关系，回答：如果给你任意8个相同的长方形，你能否拼成类似图1和图2的图形？说出你的理由．
（1）请你求出图1中y与x的函数关系式；
（2）求出图2中y与x的函数关系式；
（3）在图3中作出两个函数的图象，写出交点坐标，并解释交点坐标的实际意义；
（4）根据以上讨论完成下表，观察x与y的关系，回答：如果给你任意8个相同的长方形，你能否拼成类似图1和图2的图形？说出你的理由．
| 图（2）中小正方形边长 | 1 | 2 | 3 | 4 | … |
| x | 3 | 6 | 9 | 12 | … |
| y | 5 | 10 | 15 | 20 | … |
张师傅在铺地板时发现，用8块大小一样的长方形瓷砖恰好可以拼成一个大的长方形，如图（1）．然后，他用这8块瓷砖又拼出一个正方形，如图（2），中间恰好空出一个小正方形（阴影部分），假设长方形的长为
，宽为
，且
．
（1）求图（1）中与的函数关系式；
（2）若阴影小正方形边长为1，求图（2）中与的函数关系式；
（3）在图（3）中作出（1）、（2）中两个函数的图象，写出交点坐标，并解释交点坐标的实际意义；
（4）根据以上研究完成下表：
| 图（2）中小正方形边长 | 1 | 2 | 3 | 4 | … |
|
|
| 6 |
|
| … |
|
|
| 10 |
|
| … |
观察上表，设图（2）中小正方形边长为
，请分别猜想与、与的关系，并证明你的猜
这张师傅在铺地板时发现：用8个大小一样的长方形瓷砖恰好可以拼成一个大的长方形（如图），然后，他用这8块瓷砖七拼八凑，又拼出了一个正方形，中间还留下一个2cm×2cm的小正方形（阴影部分）．请你根据提供的信息，求出这些长方形的长和宽．