题目内容
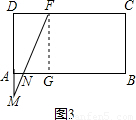
(2010•东莞)如图(1),(2)所示,矩形ABCD的边长AB=6,BC=4,点F在DC上,DF=2.动点M、N分别从点D、B同时出发,沿射线DA、线段BA向点A的方向运动(点M可运动到DA的延长线上),当动点N运动到点A时,M、N两点同时停止运动.连接FM、FN,当F、N、M不在同一直线时,可得△FMN,过△FMN三边的中点作△PWQ.设动点M、N的速度都是1个单位/秒,M、N运动的时间为x秒.试解答下列问题:(1)说明△FMN∽△QWP;
(2)设0≤x≤4(即M从D到A运动的时间段).试问x为何值时,△PWQ为直角三角形?当x在何范围时,△PQW不为直角三角形?
(3)问当x为何值时,线段MN最短?求此时MN的值.
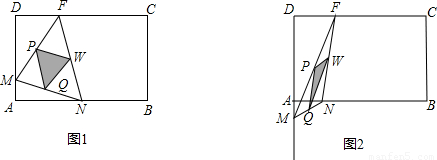
【答案】分析:(1)由平行线的性质可得∠QPW=∠MNF,∠PQW=NFM,故有△FMN∽△QWP;
(2)当△FMN是直角三角形时,△QWP也为直角三角形,当MF⊥FN时,证得△DFM∽△GFN,有DF:FG=DM:GN,得到4-x=2x,求得x此时的值,当MG⊥FN时,点M与点A重合,点N与点G重合,此时x=AD=4;
(3)当点F、M、N在同一直线上时,MN最短,设经过的时间为x,AM的长度为(4-x),AN的长度为(6-x),再由△MAN∽△MBF即可求出答案.
解答:解:(1)根据三角形中位线定理得 PQ∥FN,PW∥MN,
∴∠QPW=∠PWF,∠PWF=∠MNF,
∴∠QPW=∠MNF.
同理∠PQW=∠NFM,
∴△FMN∽△QWP;
(2)由于△FMN∽△QWP,故当△QWP是直角三角形时,△FMN也为直角三角形.
作FG⊥AB,则四边形FCBG是正方形,有GB=CF=CD-DF=4,GN=GB-BN=4-x,DM=x,
①当MF⊥FN时,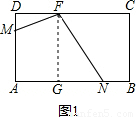
∵∠DFM+∠MFG=∠MFG+∠GFN=90°,
∴∠DFM=∠GFN.
∵∠D=∠FGN=90°,
∴△DFM∽△GFN,
∴DF:FG=DM:GN=2:4=1:2,
∴GN=2DM,
 ∴4-x=2x,
∴4-x=2x,
∴x= ;
;
②当MN⊥FN时,点M与点A重合,点N与点G重合,
∴x=AD=GB=4.
∴当x=4或 时,△QWP为直角三角形,当0≤x<
时,△QWP为直角三角形,当0≤x< ,
, <x<4时,△QWP不为直角三角形.
<x<4时,△QWP不为直角三角形.
 (3)①当0≤x≤4,即M从D到A运动时,只有当x=4时,MN的值最小,等于2;
(3)①当0≤x≤4,即M从D到A运动时,只有当x=4时,MN的值最小,等于2;
②当4<x≤6时,MN2=AM2+AN2=(x-4)2+(6-x)2
=2(x-5)2+2
当x=5时,MN2=2,故MN取得最小值 ,
,
故当x=5时,线段MN最短,MN= .
.
点评:本题为动点变化的题,主要利用了相似三角形的判定和性质,平行线的性质求解.
(2)当△FMN是直角三角形时,△QWP也为直角三角形,当MF⊥FN时,证得△DFM∽△GFN,有DF:FG=DM:GN,得到4-x=2x,求得x此时的值,当MG⊥FN时,点M与点A重合,点N与点G重合,此时x=AD=4;
(3)当点F、M、N在同一直线上时,MN最短,设经过的时间为x,AM的长度为(4-x),AN的长度为(6-x),再由△MAN∽△MBF即可求出答案.
解答:解:(1)根据三角形中位线定理得 PQ∥FN,PW∥MN,
∴∠QPW=∠PWF,∠PWF=∠MNF,
∴∠QPW=∠MNF.
同理∠PQW=∠NFM,
∴△FMN∽△QWP;
(2)由于△FMN∽△QWP,故当△QWP是直角三角形时,△FMN也为直角三角形.
作FG⊥AB,则四边形FCBG是正方形,有GB=CF=CD-DF=4,GN=GB-BN=4-x,DM=x,
①当MF⊥FN时,

∵∠DFM+∠MFG=∠MFG+∠GFN=90°,
∴∠DFM=∠GFN.
∵∠D=∠FGN=90°,
∴△DFM∽△GFN,
∴DF:FG=DM:GN=2:4=1:2,
∴GN=2DM,
 ∴4-x=2x,
∴4-x=2x,∴x=
 ;
;②当MN⊥FN时,点M与点A重合,点N与点G重合,
∴x=AD=GB=4.
∴当x=4或
 时,△QWP为直角三角形,当0≤x<
时,△QWP为直角三角形,当0≤x< ,
, <x<4时,△QWP不为直角三角形.
<x<4时,△QWP不为直角三角形. (3)①当0≤x≤4,即M从D到A运动时,只有当x=4时,MN的值最小,等于2;
(3)①当0≤x≤4,即M从D到A运动时,只有当x=4时,MN的值最小,等于2;②当4<x≤6时,MN2=AM2+AN2=(x-4)2+(6-x)2
=2(x-5)2+2
当x=5时,MN2=2,故MN取得最小值
 ,
,故当x=5时,线段MN最短,MN=
 .
.点评:本题为动点变化的题,主要利用了相似三角形的判定和性质,平行线的性质求解.

练习册系列答案
相关题目