题目内容
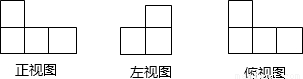
 如图为由一些边长为1cm正方体堆积在桌面形成的立方体的三视图,则该立方体露在外面部分的表面积是________ cm2.
如图为由一些边长为1cm正方体堆积在桌面形成的立方体的三视图,则该立方体露在外面部分的表面积是________ cm2.
- A.11
- B.15
- C.18
- D.22
C
分析:由俯视图可得最底层正方体的个数,由正视图和左视图可得第二层几何体的个数,进而分上,前,后,左,右等5个面求得该几何体露在外面部分的表面积即可.
解答:∵俯视图中有4个正方形,
∴组合几何体的最底层有4个正方体,
由正视图和左视图可得俯视图第二层只有1个正方体,在俯视图从上边数第二行,从左边数第一列的正方体上面,
∵正方体的边长为1,
∴正方形的面积为1.
∵上面有4个正方形,左面和右面共有2×3=6个正方形,前面和后面共有2×4=8个正方形,
∴共有18个正方形,
∴该几何体露在外面部分的表面积是18cm2.
故选C.
点评:考查由三视图判断几何体;得到组合几何体的摆放方式是解决本题的关键;用到的知识点为:俯视图打地基,主视图疯狂盖,左视图拆违章.
分析:由俯视图可得最底层正方体的个数,由正视图和左视图可得第二层几何体的个数,进而分上,前,后,左,右等5个面求得该几何体露在外面部分的表面积即可.
解答:∵俯视图中有4个正方形,
∴组合几何体的最底层有4个正方体,
由正视图和左视图可得俯视图第二层只有1个正方体,在俯视图从上边数第二行,从左边数第一列的正方体上面,
∵正方体的边长为1,
∴正方形的面积为1.
∵上面有4个正方形,左面和右面共有2×3=6个正方形,前面和后面共有2×4=8个正方形,
∴共有18个正方形,
∴该几何体露在外面部分的表面积是18cm2.
故选C.
点评:考查由三视图判断几何体;得到组合几何体的摆放方式是解决本题的关键;用到的知识点为:俯视图打地基,主视图疯狂盖,左视图拆违章.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
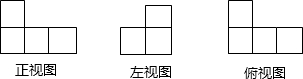 如图为由一些边长为1cm正方体堆积在桌面形成的立方体的三视图,则该立方体露在外面部分的表面积是________ cm2.
如图为由一些边长为1cm正方体堆积在桌面形成的立方体的三视图,则该立方体露在外面部分的表面积是________ cm2.