题目内容
如果两个三角形不仅是相似三角形,而且每组对应点所在的直线都经过同一个点,对应边平行,那么这两个三角形也是位似三角形,它们的相似比是位似比,这个点是位似中心,利用三角形的位似可以将一个三角形缩小或放大。
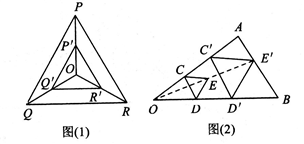
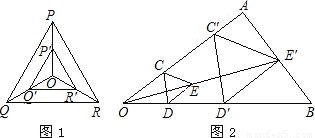
(1)如图(1)所示,点O是等边三角形PQR的中心,P′、Q′、R′分别是OP、OQ、OR的中点,则△P′Q′R′与△PQR是位似三角形,此时△P′Q′R′与△PQR的位似比、位似中心分别为( )
A.2、点P
B.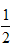 、点P
、点P
C.2、点O
D.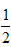 、点O
、点O
(2)如图(2)所示,用下面的方法可以画△AOB的内接等边三角形,阅读后证明相应问题。
画法:
①在△ABO内画等边△CDE,使点C在OA上,点D在OB上;
②连接OE并延长,交AB于点E′,过点E′作E′C′∥EC,交OA于点C′,作E'D′∥ED,交OB于点D′;
③连接C′D′,则△C′D′E′是△AOB的内接等边三角形,试说明△C′D′E′是等边三角形。
A.2、点P
B.
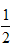 、点P
、点PC.2、点O
D.
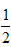 、点O
、点O(2)如图(2)所示,用下面的方法可以画△AOB的内接等边三角形,阅读后证明相应问题。
画法:
①在△ABO内画等边△CDE,使点C在OA上,点D在OB上;
②连接OE并延长,交AB于点E′,过点E′作E′C′∥EC,交OA于点C′,作E'D′∥ED,交OB于点D′;
③连接C′D′,则△C′D′E′是△AOB的内接等边三角形,试说明△C′D′E′是等边三角形。
解:(1)D;
(2)由E′C′∥EC得△OE′C′∽△OEC,
∴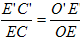 ,∠OE′C′=∠OEC,
,∠OE′C′=∠OEC,
同理: ,∠OE′D′=∠OED,
,∠OE′D′=∠OED,
∴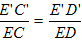 ,∠C′E′D′=∠CED,
,∠C′E′D′=∠CED,
∴△C′D′E′∽△CDE,
故△C′D′E′为等边三角形。
(2)由E′C′∥EC得△OE′C′∽△OEC,
∴
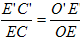 ,∠OE′C′=∠OEC,
,∠OE′C′=∠OEC,同理:
 ,∠OE′D′=∠OED,
,∠OE′D′=∠OED,∴
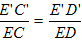 ,∠C′E′D′=∠CED,
,∠C′E′D′=∠CED,∴△C′D′E′∽△CDE,
故△C′D′E′为等边三角形。

练习册系列答案
 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
 .
. 、点P,( C)2、点O,(D)
、点P,( C)2、点O,(D)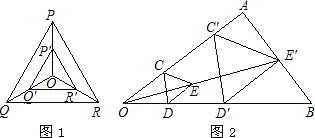 .
. 、点P,( C)2、点O,(D)
、点P,( C)2、点O,(D) 、点O;
、点O;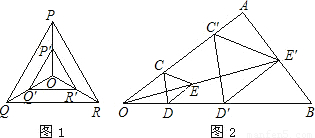
 、点P,( C)2、点O,(D)
、点P,( C)2、点O,(D) 、点O;
、点O;