题目内容
在一个长为50米,宽为30米的矩形空地上修筑同样宽的道路,使余下的部分种植花草,且使花草的总面积是道路面积的3倍.
(1)如果修两条路,使种植花草的部分为四块矩形,试画出设计图,并计算出路宽是多少?
(2)如果修一条路,使种植花草的部分为两块全等的三角形,试画出设计图,并计算出路宽是多少?
(1)如果修两条路,使种植花草的部分为四块矩形,试画出设计图,并计算出路宽是多少?
(2)如果修一条路,使种植花草的部分为两块全等的三角形,试画出设计图,并计算出路宽是多少?
分析:(1)设道路的宽为x米,利用面积之间的等量关系列出一元二次方程求解即可;
(2)首先求得线段CN的长,然后利用勾股定理求得线段BN的长,作NH⊥DM于H,利用相似三角形的对应边的比相等列出等式求得NH的长即可.
(2)首先求得线段CN的长,然后利用勾股定理求得线段BN的长,作NH⊥DM于H,利用相似三角形的对应边的比相等列出等式求得NH的长即可.
解答: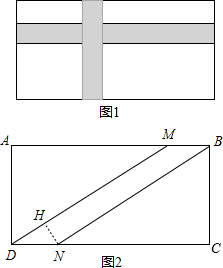 解:(1)如图1,设路宽为x米,则(30-x)(50-x)=
解:(1)如图1,设路宽为x米,则(30-x)(50-x)=
×30×50
整理得:x2-80x+375=0
解得:x=75(舍去)或x=5,
答:道路的宽为5米;
(2)如图2,设CN=x,则30x=
×30×50
解得:x=
∴DN=50-
=
∴BN=
=
作NH⊥DM于H,
由BN•NH=DN•BC
可得:NH=
,
答:道路的宽为
米;
 解:(1)如图1,设路宽为x米,则(30-x)(50-x)=
解:(1)如图1,设路宽为x米,则(30-x)(50-x)=| 3 |
| 4 |
整理得:x2-80x+375=0
解得:x=75(舍去)或x=5,
答:道路的宽为5米;
(2)如图2,设CN=x,则30x=
| 3 |
| 4 |
解得:x=
| 75 |
| 2 |
∴DN=50-
| 75 |
| 2 |
| 25 |
| 2 |
∴BN=
302+(
|
| 15 |
| 2 |
| 41 |
作NH⊥DM于H,
由BN•NH=DN•BC
可得:NH=
50
| ||
| 41 |
答:道路的宽为
50
| ||
| 41 |
点评:本题考查了一元二次方程的应用,特别是图形的面积问题更是一元二次方程的应用中考查的重点知识.

练习册系列答案
相关题目