题目内容
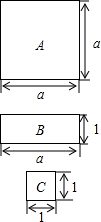 如图,有A型、B型、C型三种不同的纸板,其中
如图,有A型、B型、C型三种不同的纸板,其中A型:边长为a厘米的正方形;
B型:长为a厘米,宽为1厘米的长方形;
C型:边长为1厘米的正方形.
(1)A型2块,B型4块,C型4块,此时纸板的总面积为
(2a2+4a+4)
(2a2+4a+4)
平方厘米;①从这10块纸板中拿掉1块A型纸板,剩下的纸板在不重叠的情况下,可以紧密的排出一个大正方形.剩下纸板的总面积为
(a2+4a+4)
(a2+4a+4)
平方厘米,这个大正方形的边长为(a+2)
(a+2)
厘米;②从这10块纸板中拿掉2块同类型的纸板,使得剩下的纸板在不重叠的情况下,可以紧密地排出两个相同的大正方形,请问拿掉的是2块哪种类型的纸板?(计算说明)
(2)A型12块,B型12块,C型4快.从这28块纸板中拿掉1块纸板,使得剩下的纸板在不重叠的情况下,可以紧密地排出三个相同形状的大正方形,则大正方形的边长为
(2a+1)cm
(2a+1)cm
.分析:(1)由于1块A型的面积为a2cm,1快、块B型的面积为4acm2,1块C型的面积为4cm2,所以A型2块,B型4块,C型4块的总面积为(2a2+4a+4)cm2;
①把2a2+4a+4减去a2,然后根据完全平方公式得到a2+4a+4=(a+2)2,由此得到正方形的边长;
②把2a2+4a+4减去2,然后根据完全平方公式得到2a2+4a+2=2(a+1)2,由此得到正方形的边长,所以从这10块纸板中拿掉2块C类型的纸板满足要求;
(2)从这28块纸板中拿掉1块C类型的纸板可满足要求,因为12a2+12a+4-1=12a2+12a+3=3(2a+1)2,此时正方形的边长为(2a+1)cm.
①把2a2+4a+4减去a2,然后根据完全平方公式得到a2+4a+4=(a+2)2,由此得到正方形的边长;
②把2a2+4a+4减去2,然后根据完全平方公式得到2a2+4a+2=2(a+1)2,由此得到正方形的边长,所以从这10块纸板中拿掉2块C类型的纸板满足要求;
(2)从这28块纸板中拿掉1块C类型的纸板可满足要求,因为12a2+12a+4-1=12a2+12a+3=3(2a+1)2,此时正方形的边长为(2a+1)cm.
解答:解:(1)1块A型的面积为a2cm,1快、块B型的面积为4acm2,1块C型的面积为4cm2,所以A型2块,B型4块,C型4块的总面积为(2a2+4a+4)cm2;
①这10块纸板中拿掉1块A型纸板,剩下的纸板在不重叠的情况下,可以紧密的排出一个大正方形.剩下纸板的总面积为2a2+4a+4-a2=a2+4a+4,而a2+4a+4=(a+2)2,则此正方形的边长为(a+2)cm;
②从这10块纸板中拿掉2块C类型的纸板,使得剩下的纸板在不重叠的情况下,可以紧密地排出两个相同的大正方形.理由如下:
2a2+4a+4-2=2a2+4a+2=2(a2+2a+1)=2(a+1)2,此时正方形的边长为(a+1)cm;
(2)12a2+12a+4-1=12a2+12a+3=3(2a+1)2,此时正方形的边长为(2a+1)cm.
故答案为(2a2+4a+4),(a2+4a+4),a+2;(2a+1)cm.
①这10块纸板中拿掉1块A型纸板,剩下的纸板在不重叠的情况下,可以紧密的排出一个大正方形.剩下纸板的总面积为2a2+4a+4-a2=a2+4a+4,而a2+4a+4=(a+2)2,则此正方形的边长为(a+2)cm;
②从这10块纸板中拿掉2块C类型的纸板,使得剩下的纸板在不重叠的情况下,可以紧密地排出两个相同的大正方形.理由如下:
2a2+4a+4-2=2a2+4a+2=2(a2+2a+1)=2(a+1)2,此时正方形的边长为(a+1)cm;
(2)12a2+12a+4-1=12a2+12a+3=3(2a+1)2,此时正方形的边长为(2a+1)cm.
故答案为(2a2+4a+4),(a2+4a+4),a+2;(2a+1)cm.
点评:本题考查了完全平方公式的几何背景:运用几何直观理解、解决完全平方公式的推导过程,通过几何图形之间的数量关系对完全平方公式做出几何解释.

练习册系列答案
相关题目
 如图,有A型、B型、C型三种不同类型的纸板,其中A型是边长为a的正方形,B型是长为a宽为b的长方形,C型是边长为b的正方形.
如图,有A型、B型、C型三种不同类型的纸板,其中A型是边长为a的正方形,B型是长为a宽为b的长方形,C型是边长为b的正方形.