题目内容
对于两个相似三角形,如果沿周界按对应点顺序环绕的方向相同,那么称这两个三角形互为顺相似;如果沿周界按对应点顺序环绕的方向相反,那么称这两个三角形互为逆相似。例如,如图①,△ABC∽△A’B’C’且沿周界ABCA与A’B’C’A’环绕的方向相同,因此△ABC 与△A’B’C’互为顺相似;如图②,△ABC∽△A’B’C’,且沿周界ABCA与 A’B’C’A’环绕的方向相反,因此△ABC 与△A’B’C’互为逆相似。

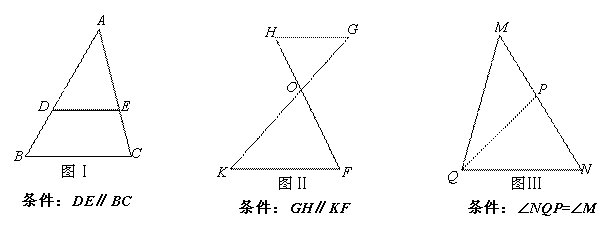
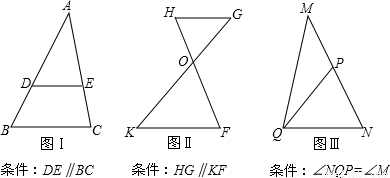
(1)根据图I、图II和图III满足的条件,可得下列三对相似三角形:①△ADE与△ABC;②△GHO与△KFO;③△NQP与△NMQ。其中,互为顺相似的是 ;互为逆相似的是 。(填写所有符合要求的序号)

(2)如图③,在锐角△ABC中,ÐA<ÐB<ÐC,点P在△ABC的边上(不与点A、B、C重合)。过点P画直线截△ABC,使截得的一个三角形与△ABC互为逆相似。请根据点P的不同位置,探索过点P的截线的情形,画出图形并说明截线满足的条件,不必说明理由。

(1)①②;③
(2)
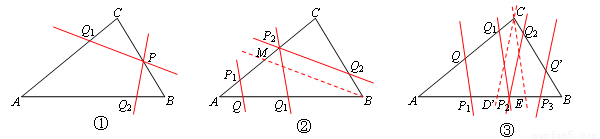
【解析】解:(1)①②;③。
(2)根据点P在△ABC边上的位置分为以下三种情况。
第一种情况:如图①,点P在BC(不含点B、C)上,过点P只能画出2条截线PQ1、PQ2,分别使ÐCPQ1=ÐA,ÐBPQ2=ÐA,此时△PQ1C、△PBQ2都与△ABC互为逆相似。
第二种情况:如图②,点P在AC(不含点A、C)上,过点B作ÐCBM=ÐA,BM交AC于点M。
当点P在AM(不含点M)上时,过点P1只能画出1条截线P1Q,使ÐAP1Q=ÐABC,此时△AP1Q与△ABC互为逆相似;
当点P在CM上时,过点P2只能画出2条截线P2Q1、P2Q2,分别使ÐAP2Q1=ÐABC,ÐCP2Q2=ÐABC,此时△AP2Q1、△Q2P2C都与△ABC互为逆相似。
第三种情况:如图③,点P在AB(不含点A、B)上,过点C作ÐBCD=ÐA,ÐACE=ÐB,CD、CE分别交AC于点D、E。
当点P在AD(不含点D)上时,过点P只能画出1条截线P1Q,使ÐAP1Q=ÐABC,此时△AQP1与△ABC互为逆相似;
当点P在DE上时,过点P2只能画出2条截线P2Q1、P2Q2,分别使ÐAP2Q1=ÐACB,ÐBP2Q2=ÐBCA,此时△AQ1P2、△Q2BP2都与△ABC互为逆相似;
当点P在BE(不含点E)上时,过点P3只能画出1条截线P3Q’,使ÐBP3Q’=ÐBCA,此时△Q’BP3与△ABC互为逆相似。

(1)根据定义作出判断。
(2)分点P在BC(不含点B、C)上、点P在AC(不含点A、C)上、点P在AB(不含点A、B)上三种情况,根据定义讨论。

 阅读快车系列答案
阅读快车系列答案






 如图②△ABC∽△A‘B‘C‘,且沿周界ABCA与A‘B‘C‘A‘环绕的方向相反,因此△ABC与△A‘B‘C‘互为逆相似;
如图②△ABC∽△A‘B‘C‘,且沿周界ABCA与A‘B‘C‘A‘环绕的方向相反,因此△ABC与△A‘B‘C‘互为逆相似;