题目内容
下表给出了代数式x2+bx+c与x的一些对应值:
| x | … | 0 | 1 | 2 | 3 | 4 | … |
| x2+bx+c | … | 3 | -1 | 3 | … |
先向右平移2个单位,再向下平移1个单位(或者先向下平移1个单位,再向右平移2个单位)
分析:先用待定系数法求出函数y=x2+bx+c的解析式,再根据“上加下减,左加右减”的原则解答即可.
解答:∵x=0时,y=3;
x=2时,y=-1;
∴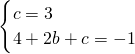 ,解得
,解得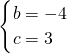 ,
,
∴所得函数的解析式为:y=x2-4x+3,即y=(x-2)2-1,
∴由上加下减,左加右减”的原则可知,函数y=x2的图象可以通过平移得到函数y=(x-2)2-1的图象先向右平移2个单位,再向下平移1个单位(或者先向下平移1个单位,再向右平移2个单位).
故答案为:先向右平移2个单位,再向下平移1个单位(或者先向下平移1个单位,再向右平移2个单位).
点评:本题考查的是二次函数的图象与几何变换及用待定系数法求二次函数的解析式,熟知“上加下减,左加右减”的原则是解答此题的关键.
分析:先用待定系数法求出函数y=x2+bx+c的解析式,再根据“上加下减,左加右减”的原则解答即可.
解答:∵x=0时,y=3;
x=2时,y=-1;
∴
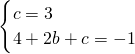 ,解得
,解得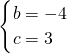 ,
,∴所得函数的解析式为:y=x2-4x+3,即y=(x-2)2-1,
∴由上加下减,左加右减”的原则可知,函数y=x2的图象可以通过平移得到函数y=(x-2)2-1的图象先向右平移2个单位,再向下平移1个单位(或者先向下平移1个单位,再向右平移2个单位).
故答案为:先向右平移2个单位,再向下平移1个单位(或者先向下平移1个单位,再向右平移2个单位).
点评:本题考查的是二次函数的图象与几何变换及用待定系数法求二次函数的解析式,熟知“上加下减,左加右减”的原则是解答此题的关键.

练习册系列答案
相关题目
下表给出了代数式x2+bx+c与x的一些对应值:
(1)请在表内的空格中填入适当的数;
(2)设y=x2+bx+c,则当x取何值时,y>0;
(3)请说明经过怎样平移函数y=x2+bx+c的图象得到函数y=x2的图象?
| x | … | 0 | 1 | 2 | 3 | 4 | … |
| x2+bx+c | … | 3 | -1 | 3 | … |
(2)设y=x2+bx+c,则当x取何值时,y>0;
(3)请说明经过怎样平移函数y=x2+bx+c的图象得到函数y=x2的图象?
下表给出了代数式x2+bx+c与x的一些对应值:
(1)根据表格中的数据,确定b、c的值,并填齐表格空白处的对应值;
(2)设y=x2+bx+c的图象与x轴的交点为A、B两点(A点在B点左侧),与y轴交于点C,P为线段AB上一动点,过P点作PE∥AC交BC于E,连接PC,当△PEC的面积最大时,求P点的坐标.
| x | … | -1 | 0 | 1 | 2 | 3 | 4 | … |
| x2+bx+c | … | 3 | -1 | 3 | … |
(2)设y=x2+bx+c的图象与x轴的交点为A、B两点(A点在B点左侧),与y轴交于点C,P为线段AB上一动点,过P点作PE∥AC交BC于E,连接PC,当△PEC的面积最大时,求P点的坐标.

下表给出了代数式x2+bx+c与x的一些对应值:
(1)根据表格中的数据,确定b、c的值,并填齐表格中空白处的对应值;
(2)代数式x2+bx+c是否有最小值?如果有,求出最小值;如果没有,请说明理由;
(3)设y=x2+bx+c的图象与x轴的交点为A、B两点(A点在B点左侧),与y轴交于点C,P点为线段AB上一动点,过P点作PE∥AC交BC于E,连接PC,当△PEC的面积最大时,求P点的坐标.
| x | … | -1 | 0 | 1 | 2 | 3 | 4 | … |
| X2+bx+c | … | 3 | -1 | 3 | … |
(2)代数式x2+bx+c是否有最小值?如果有,求出最小值;如果没有,请说明理由;
(3)设y=x2+bx+c的图象与x轴的交点为A、B两点(A点在B点左侧),与y轴交于点C,P点为线段AB上一动点,过P点作PE∥AC交BC于E,连接PC,当△PEC的面积最大时,求P点的坐标.
下表给出了代数式x2+bx+c与x的一些对应值:
函数y=x2的图象可以通过平移得到函数y=x2+bx+c的图象.请写出一种正确的平移 .
| x | … | 0 | 1 | 2 | 3 | 4 | … |
| x2+bx+c | … | 3 | -1 | 3 | … |