题目内容
阅读题：我们可以用换元法解简单的高次方程，入解方程x4-3x2+2=0可设y=x2，则原方程可化为y2-3y+2=0，解之得y1=2y2=1，当y1=2时，即x2=2则x1=
| 2 |
| 2 |
| 2 |
| 2 |
（1）已知方程（2x2+1）2-2x2-3=0，设y=2x2+1，则原方程可化为
（2）仿照上述解法解方程（x2+2x）2-3x2-6x=0．
分析：（1）利用完全平方公式可把原式变为（2x2+1）2-2x2-3=（2x2+1）2-（2x2+1）-2，然后用y代替式子中的2．
（2）（x2+2x）2-3x2-6x=0即（x2+2x）2-3（x2+2x）=0．可以把x2+2x当作整体，设x2+2x=y，原方程即可变形为关于y的方程，即可求得y的值，因而求得x的值．
（2）（x2+2x）2-3x2-6x=0即（x2+2x）2-3（x2+2x）=0．可以把x2+2x当作整体，设x2+2x=y，原方程即可变形为关于y的方程，即可求得y的值，因而求得x的值．
解答：解：（1）设y=2x2+1，
则原式左边=（2x2+1）2-（2x2+1）-2=y2-y-2．
∴原方程可化为y2-y-2=0．
（2）设x2+2x=y，
则原式左边=（x2+2x）2-3（x2+2x）=y2-3y；
∴y2-3y=0，
∴y（y-3）=0，
∴y=0或3．
当y=0时，则x2+2x=0，
∴x（x+2）=0，
∴x=-2或0；
当y=3时，则x2+2x=3，
∴x2+2x-3=0，
解得x=1或-3．
故方程的解为-3，-2，0，1．
则原式左边=（2x2+1）2-（2x2+1）-2=y2-y-2．
∴原方程可化为y2-y-2=0．
（2）设x2+2x=y，
则原式左边=（x2+2x）2-3（x2+2x）=y2-3y；
∴y2-3y=0，
∴y（y-3）=0，
∴y=0或3．
当y=0时，则x2+2x=0，
∴x（x+2）=0，
∴x=-2或0；
当y=3时，则x2+2x=3，
∴x2+2x-3=0，
解得x=1或-3．
故方程的解为-3，-2，0，1．
点评：本题的关键是把2x2+1和x2+2x看成一个整体来计算，即换元法思想．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
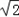、x2=-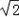
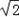、x2=﹣
，
、x2=﹣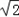
；x3=1、x4=﹣1。
、x2=-
，当y2=1时，即x2=1，则x3=1、x4=-1，故原方程的解为x1=
、x2=-
；x3=1x4=-1，仿照上面完成下面解答：