题目内容
如图,将一张正方形纸片,剪成四个大小形状一样的小正方形,然后将其中的一个小正方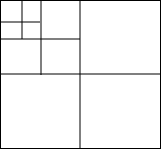 形再按同样的方法剪成四个小正方形,再将其中的一个小正方形剪成四个小正方形,如此循环进行下去;
形再按同样的方法剪成四个小正方形,再将其中的一个小正方形剪成四个小正方形,如此循环进行下去;
(1)填表:
| 剪的次数 | 1 | 2 | 3 | 4 | 5 |
| 正方形个数 | 4 | 7 |
(2)如果剪了100次,共剪出多少个小正方形?
(3)如果剪n次,共剪出多少个小正方形?
(4)能否经过若干次分割后共得到2009片纸片?若能,请直接写出相应的次数,若不能,请说明理由.
解:(1)后一个图形中的个数总比前一个图形中的个数多3个,填表如下:
| 剪的次数 | 1 | 2 | 3 | 4 | 5 |
| 正方形个数 | 4 | 7 | 10 | 13 | 16 |
(2)剪n次,共剪出小正方形的个数为:4+3(n-1)=3n+1;
(3)设经过n次分割后共得到2009片纸片.
根据题意,得3n+1=2009,3n=2008.
此时n不是整数,
所以不能.
分析:(1)剪一次是4个小正方形,以后每剪一次都是少1个多4个(即多3个)小正方形,照此填表即可;
(2)由于每剪一次都是多3个小正方形,而第一次是4个小正方形,所以剪n次,共剪出小正方形的个数为4+3(n-1)=3n+1;
(3)由(2)中的数据规律列方程,如果有正整数解,则能够;否则,就不能.
点评:本题考查规律型中的图形变化问题,同时考查学生观察、分析、归纳和应用规律的能力.

练习册系列答案
相关题目

 如图,把一张标准纸一次又一次对开,得到“2开”纸,“4开”纸,“8开”纸,“16开”纸….已知标准纸的短边长为a.
如图,把一张标准纸一次又一次对开,得到“2开”纸,“4开”纸,“8开”纸,“16开”纸….已知标准纸的短边长为a.





 如图,把一张标准纸一次又一次对开,得到“2开”纸,“4开”纸,“8开”纸,“16开”纸….已知标准纸的短边长为a.
如图,把一张标准纸一次又一次对开,得到“2开”纸,“4开”纸,“8开”纸,“16开”纸….已知标准纸的短边长为a.
