题目内容
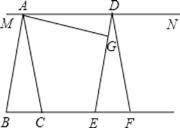
【题目】如图所示,将![]() 沿直线BC方向平移
沿直线BC方向平移![]() 的位置,G是DE上一点,连接AG,过点A、D作直线MN.
的位置,G是DE上一点,连接AG,过点A、D作直线MN.
(1)求证:![]() ;
;
(2)若![]() ,
,![]() ,判断AG与DE的位置关系,并证明你的结论.
,判断AG与DE的位置关系,并证明你的结论.
【答案】(1)见解析;(2)见解析.
【解析】(1)利用平移的性质得到AB与DE平行且相等,得到四边形ABED为平行四边形,利用平行四边形的性质得到对角相等,利用外角性质即可得证;
(2)AG垂直与DE,理由为:由平移的性质得到∠EDF=∠BAC,根据∠EDF=∠DAG,等量代换得到∠BAC=∠DAG,由AB与DE平行,利用两直线平行同旁内角互补得到一对角互补,等量代换得到∠ABC=∠CAG,利用等式的性质及平行线的性质即可得证.
(1)由平移的性质得:△ABC≌△DEF,
∴AB=DE,AB∥DE,
∴四边形ABED为平行四边形,
∴AD∥BF,∠ADG=∠ABC,
∴∠ADG=∠DEF,
∴∠ABC=∠DEF=∠ADG,
∵∠AGE为△ADG的外角,
∴∠AGE=∠DAG+∠ADG=∠GAD+∠ABC;
(2)AG⊥DE,理由为:
由平移的性质得到∠EDF=∠BAC,
∵∠EDF=∠DAG,
∴∠BAC=∠DAG,
∵AB∥DE,
∴∠ABC+∠BEG=180°,
∵∠CAG+∠CEG=180°,
∴∠ABC=∠CAG,
∵MN∥BC,∴∠ABC=∠MAB,
∴∠MAB=∠CAG,
∵∠MAB+∠BAC+∠CAG+∠DAG=180°,
∴∠CAG+∠BAC=90°,即∠BAG=90°,
∵AB∥DE,
∴∠BAG+∠AGD=90°,
则AG⊥DE.

 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案【题目】随着我市社会经济的发展和交通状况的改善,我市的旅游业得到了高速发展![]() 某旅游公司对我市一企业个人旅游年消费情况进行问卷调查
某旅游公司对我市一企业个人旅游年消费情况进行问卷调查![]() 随机抽取部分员工,记录每个人年消费金额,并将调查数据适当整理,绘制成如下两幅尚不完整的表和图:
随机抽取部分员工,记录每个人年消费金额,并将调查数据适当整理,绘制成如下两幅尚不完整的表和图:
组别 | 个人年消费金额 | 频数 | 频率 |
A |
| 18 |
|
B |
| a | b |
C |
|
|
|
D |
| 24 |
|
E |
| 12 |
|
合计 | c |
| |

根据以上信息解答下列问题:
![]() ________;
________; ![]() ________;
________; ![]() ________;
________;
![]() 补全频数分布直方图;
补全频数分布直方图;
![]() 若这个企业有3000名员工,请你估计个人旅游年消费金额在6000元以上的人数.
若这个企业有3000名员工,请你估计个人旅游年消费金额在6000元以上的人数.