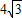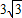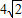题目内容
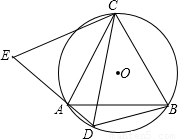
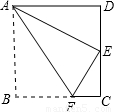
(2007•莱芜)如图,△ABC是⊙O的内接三角形,AC=BC,D为⊙O中 上一点,延长DA至点E,使CE=CD.
上一点,延长DA至点E,使CE=CD.(1)求证:AE=BD;
(2)若AC⊥BC,求证:AD+BD=
 CD.
CD.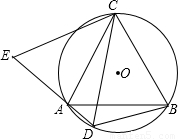
【答案】分析:(1)先证出△AEC≌△BDC,只要再找一对角相等就可以了,利用边相等,可得∠CAB=∠CBA,∠CEA=∠CDE,而∠CAB=∠CDB=∠CDE,故∠CEA=∠CDB,(CE=CD,∠CAE=∠CBD)再利用SAS可证出△AEC≌△BDC.
(2)利用(1)中的全等,可得,AE=BD,∠ECA=∠DCB,那么就有∠ECD=∠ECA+∠ACD=90°,根据勾股定理得DE=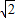 CD,而DE=AD+AE=AD+BG,所以有AD+BD=
CD,而DE=AD+AE=AD+BG,所以有AD+BD=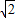 CD.
CD.
解答:证明:(1)∵△ABC是⊙O的内接三角形,AC=BC,
∴∠ABC=∠BAC,
∵CE=CD,
∴∠CDE=∠CED;
又∵∠ABC=∠CDE,
∴∠ABC=∠BAC=∠CDE=∠CED,(同弧上的圆周角相等)
∴∠ACB=∠DCE,
∴∠BCD=∠ACE,
AC=BC,∠ACE=∠BCD,CE=CD;
在△AEC和△BDC中,
∴△AEC≌△BDC(SAS),
∴AE=BD.

(2)∵AC⊥BC,
∴∠ACB=90°,
∴∠DCE=90°;
又∵CD=CE,
∴△DCE为等腰直角三角形,
∴DE= CD,
CD,
又∵DE=AD+AE且AE=BD,
∴AD+BD=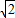 CD.
CD.
点评:本题利用了同弧上的圆周角相等,全等三角形的判定和性质,等腰直角三角形的性质,勾股定理,还有圆内接四边形的外角等于其内对角等知识.
(2)利用(1)中的全等,可得,AE=BD,∠ECA=∠DCB,那么就有∠ECD=∠ECA+∠ACD=90°,根据勾股定理得DE=
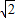 CD,而DE=AD+AE=AD+BG,所以有AD+BD=
CD,而DE=AD+AE=AD+BG,所以有AD+BD=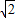 CD.
CD.解答:证明:(1)∵△ABC是⊙O的内接三角形,AC=BC,
∴∠ABC=∠BAC,
∵CE=CD,
∴∠CDE=∠CED;
又∵∠ABC=∠CDE,
∴∠ABC=∠BAC=∠CDE=∠CED,(同弧上的圆周角相等)
∴∠ACB=∠DCE,
∴∠BCD=∠ACE,
AC=BC,∠ACE=∠BCD,CE=CD;
在△AEC和△BDC中,
∴△AEC≌△BDC(SAS),
∴AE=BD.

(2)∵AC⊥BC,
∴∠ACB=90°,
∴∠DCE=90°;
又∵CD=CE,
∴△DCE为等腰直角三角形,
∴DE=
 CD,
CD,又∵DE=AD+AE且AE=BD,
∴AD+BD=
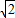 CD.
CD.点评:本题利用了同弧上的圆周角相等,全等三角形的判定和性质,等腰直角三角形的性质,勾股定理,还有圆内接四边形的外角等于其内对角等知识.

练习册系列答案
相关题目
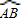 上一点,延长DA至点E,使CE=CD.
上一点,延长DA至点E,使CE=CD.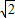 CD.
CD.
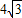
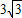
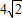
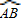 上一点,延长DA至点E,使CE=CD.
上一点,延长DA至点E,使CE=CD.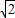 CD.
CD.