题目内容
9、如图是小明设计用手电来测量某古城墙高度的示意图，点P处放一水平的平面镜，光线从点A出发经平面镜反射后刚好射到古城墙CD的顶端C处，已知AB⊥BD，CD⊥BD，且测得AB=1.2米，BP=1.8米，PD=12米，那么该古城墙的高度是8
米．分析：直角三角形ABP和直角三角形PCD相似，即1.2：1.8=CD：12求得该古城墙的高度．
解答：解：由题意知：光线AP与光线PC，∠APB=∠CPD，
所以Rt△ABP∽Rt△PCD，
所以AB：BP=CD：PD
即1.2：1.8=CD：12，
解得CD=8米．
故答案为：8．
所以Rt△ABP∽Rt△PCD，
所以AB：BP=CD：PD
即1.2：1.8=CD：12，
解得CD=8米．
故答案为：8．
点评：本题考查了相似三角形的应用，从三角形ABP和三角形PCD相似，即求得PD．
练习册系列答案
阅读快车系列答案
相关题目
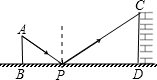如图是小明设计用手电来测量某古城墙高度的示意图．点P处放一水平的平面镜，光线从点A出发经平面镜反射后刚好射到古城墙CD的顶端C处，已知AB⊥BD，CD⊥BD，且测得AB=1.2米，BP=1.8米，PD=12米，那么该古城墙的高度是（ ）| A、6米 | B、8米 | C、18米 | D、24米 |
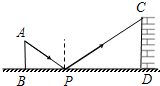如图是小明设计用手电来测量某古城墙高度的示意图．点P处放一水平的平面镜，光线从点A出发经平面镜反射后刚好射到古城墙CD的顶端C处，已知AB⊥BD，CD⊥BD，且测得AB=1.2米，BP=1.8米，PD=15米，那么该古城墙的高度是
