Question

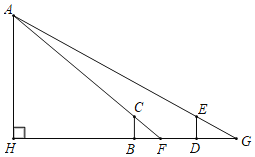
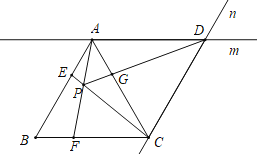
【题目】如图，在等边△ABC中，点E，F分别是边AB，BC上的动点（不与端点重合），且始终保持AE＝BF，连接AF，CE相交于点P过点A作直线m∥BC，过点C作直线n∥AB，直线m，n相交于点D，连接PD交AC于点G，在点E，F的运动过程中，若＝，则的值为_____．

Answer 1

【答案】，

【解析】

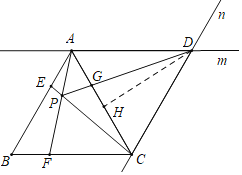
作DH⊥AC于H，由“SAS”可证△ABF≌△CAE，可得∠BAF＝∠ACE，可求∠CPF＝60°，通过证明A，P，C，D四点共圆，可得∠ACP＝∠ADP，∠APD＝∠ACD＝60°，通过证明△DAG∽△DPA，可得DA2＝DGDP＝20k2，可求DA的长，由勾股定理可求GH的长，即可求解．

解：作DH⊥AC于H，

∵△ABC是等边三角形，

∴AC＝AB，∠B＝∠CAE＝60°，且AE＝BF，

∴△ABF≌△CAE（SAS），

∴∠BAF＝∠ACE，

∴∠CPF＝∠ACP+∠CAP＝∠BAF+∠CAP＝∠CAB＝60°，

∵m∥BC，n∥AB，

∴∠DAC＝∠ACB＝60°，∠ACD＝∠BAC＝60°，

∴△ADC是等边三角形，

∴∠ADC＝60°，

∵∠APC+∠ADC＝180°，

∴A，P，C，D四点共圆，

∴∠ACP＝∠ADP，∠APD＝∠ACD＝60°

∵

∴可以假设PG＝k，DG＝4k，

∵∠ADG＝∠ADP，∠DAG＝∠DPA＝60°，

∴△DAG∽△DPA，

∴DA2＝DGDP＝20k2，

∵DA＞0

∴

∴

在Rt△DGH中，

∴

∴

当点G在点H下方时，根据对称性可得：

故答案为：，．