题目内容
已知函数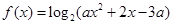 ,
,(Ⅰ)当
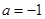 时,求该函数的定义域和值域;
时,求该函数的定义域和值域;(Ⅱ)如果
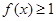 在区间
在区间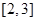 上恒成立,求实数
上恒成立,求实数 的取值范围
的取值范围
解:(1) 当 时,
时,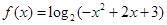
令 ,解得
,解得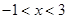
所以函数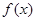 的定义域为
的定义域为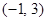 .
.
令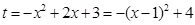 ,则
,则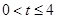
所以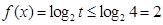
因此函数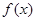 的值域为
的值域为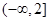 6分
6分
(2) 解法一: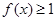 在区间
在区间 上恒成立等价于
上恒成立等价于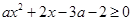 在区间
在区间 上恒成立
上恒成立
令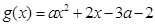
当 时,
时,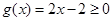 ,所以
,所以 满足题意.
满足题意.
当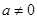 时,
时,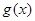 是二次函数,对称轴为
是二次函数,对称轴为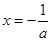 ,
,
当 时,
时,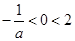 ,函数
,函数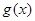 在区间
在区间 上是增函数,
上是增函数,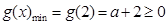 ,解得
,解得 ;
;
当 时,
时, ,
,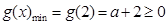 ,解得
,解得
当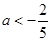 时,
时,
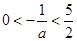 ,
,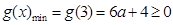 ,解得
,解得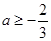
综上, 的取值范围是
的取值范围是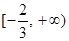 12分
12分
解法二: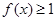 在区间
在区间 上恒成立等价于
上恒成立等价于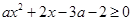 在区间
在区间 上恒成立
上恒成立
由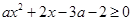 且
且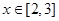 时,
时,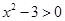 ,得
,得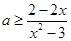
令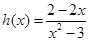 ,则
,则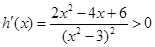
所以 在区间
在区间 上是增函数,所以
上是增函数,所以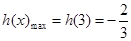
因此 的取值范围是
的取值范围是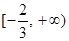 . 12分解析:
. 12分解析:
略
 时,
时,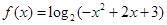
令
 ,解得
,解得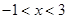
所以函数
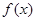 的定义域为
的定义域为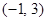 .
.令
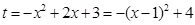 ,则
,则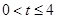
所以
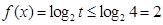
因此函数
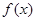 的值域为
的值域为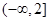 6分
6分(2) 解法一:
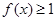 在区间
在区间 上恒成立等价于
上恒成立等价于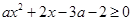 在区间
在区间 上恒成立
上恒成立令
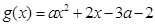
当
 时,
时,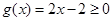 ,所以
,所以 满足题意.
满足题意.当
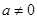 时,
时,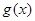 是二次函数,对称轴为
是二次函数,对称轴为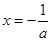 ,
,当
 时,
时,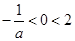 ,函数
,函数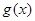 在区间
在区间 上是增函数,
上是增函数,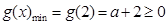 ,解得
,解得 ;
;当
 时,
时, ,
,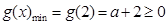 ,解得
,解得
当
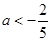 时,
时,
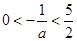 ,
,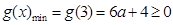 ,解得
,解得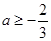
综上,
 的取值范围是
的取值范围是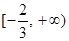 12分
12分解法二:
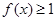 在区间
在区间 上恒成立等价于
上恒成立等价于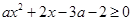 在区间
在区间 上恒成立
上恒成立由
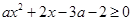 且
且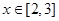 时,
时,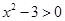 ,得
,得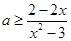
令
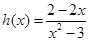 ,则
,则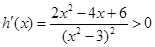
所以
 在区间
在区间 上是增函数,所以
上是增函数,所以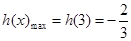
因此
 的取值范围是
的取值范围是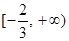 . 12分解析:
. 12分解析:略

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
 时,求y的值.
时,求y的值.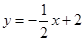 ,当
,当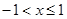 时,y的取值范围是
( )
时,y的取值范围是
( )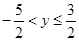 (B)
(B)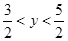
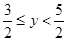 (D)
(D)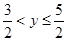
 与
与 成正比例,且当
成正比例,且当 时,
时, ;
; 与
与 之间的函数关系式;
之间的函数关系式; 时,求
时,求