题目内容
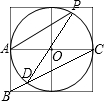 如图,四个边长为1的小正方形拼成一个大正方形,A、B、C、O是小正方形顶点,⊙O的半径为1,P是⊙O上的点,且位于右上方的小正方形内,BC与⊙O相交于点D,则tan∠APD等于
如图,四个边长为1的小正方形拼成一个大正方形,A、B、C、O是小正方形顶点,⊙O的半径为1,P是⊙O上的点,且位于右上方的小正方形内,BC与⊙O相交于点D,则tan∠APD等于
- A.2
- B.1
- C.

- D.
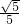
C
分析:根据题意知,A、D、C、P四点共圆,所以由圆周角定理得到∠APD=∠ACD,所以在直角三角形ABC中根据锐角三角函数的定义求tan∠APD.
解答:根据题意知,A、D、C、P四点共圆,
∴∠APD=∠ACD(同弧所对的圆周角相等);
又∵A、B、C、O是小正方形顶点,
∴AB=AO=OC,∠BAC=90°,
∴tan∠APD=tan∠ACD=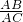 =
= .
.
故选C.
点评:本题考查了锐角三角函数的定义、圆周角定理.在直角三角形中,正切等于对边比邻边.
分析:根据题意知,A、D、C、P四点共圆,所以由圆周角定理得到∠APD=∠ACD,所以在直角三角形ABC中根据锐角三角函数的定义求tan∠APD.
解答:根据题意知,A、D、C、P四点共圆,
∴∠APD=∠ACD(同弧所对的圆周角相等);
又∵A、B、C、O是小正方形顶点,
∴AB=AO=OC,∠BAC=90°,
∴tan∠APD=tan∠ACD=
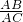 =
= .
.故选C.
点评:本题考查了锐角三角函数的定义、圆周角定理.在直角三角形中,正切等于对边比邻边.

练习册系列答案
相关题目
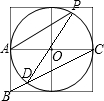 如图,四个边长为1的小正方形拼成一个大正方形,A、B、C、O是小正方形顶点,⊙O的半径为1,P是⊙O上的点,且位于右上方的小正方形内,BC与⊙O相交于点D,则tan∠APD等于( )
如图,四个边长为1的小正方形拼成一个大正方形,A、B、C、O是小正方形顶点,⊙O的半径为1,P是⊙O上的点,且位于右上方的小正方形内,BC与⊙O相交于点D,则tan∠APD等于( )| A、2 | ||||
| B、1 | ||||
C、
| ||||
D、
|
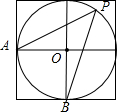 如图,四个边长为2的小正方形拼成一个大正方形,A、B、O是小正方形顶点,⊙O的半径为2,P是⊙O上的点,且位于右上方的小正方形内,则∠APB等于( )
如图,四个边长为2的小正方形拼成一个大正方形,A、B、O是小正方形顶点,⊙O的半径为2,P是⊙O上的点,且位于右上方的小正方形内,则∠APB等于( )| A、30° | B、45° | C、60° | D、90° |
 如图,四个边长为1的小正方形拼成一个大正方形,P是⊙O上的点,OA、OB为半径,则∠APB等于( )
如图,四个边长为1的小正方形拼成一个大正方形,P是⊙O上的点,OA、OB为半径,则∠APB等于( )| A、90° | B、60° | C、45° | D、30° |
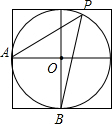 如图,四个边长为1的小正方形拼成一个大正方形,A、B、O是小正方形顶点,⊙O的半径为1,P是⊙O上的点,且位于右上方的小正方形内,则∠APB的度数为
如图,四个边长为1的小正方形拼成一个大正方形,A、B、O是小正方形顶点,⊙O的半径为1,P是⊙O上的点,且位于右上方的小正方形内,则∠APB的度数为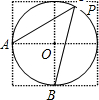 如图,四个边长为1的小正方形拼成一个大正方形,A、B、O是小正方形顶点,⊙O的半径为1,P是⊙O上的点,且位于右上方的小正方形内,则sin∠APB等于( )
如图,四个边长为1的小正方形拼成一个大正方形,A、B、O是小正方形顶点,⊙O的半径为1,P是⊙O上的点,且位于右上方的小正方形内,则sin∠APB等于( )