题目内容
![]()
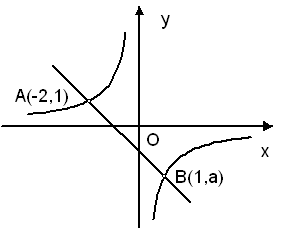
(1)利用图象中的条件,求反比例函数和一次函数的解析式;
(2)根据图象写出使一次函数的值大于反比例函数的x的取值范围.
练习册系列答案
相关题目
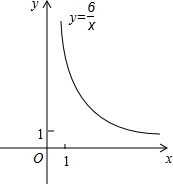 如图,平面直角坐标系xOy中,点pn(xn,yn)在双曲线
如图,平面直角坐标系xOy中,点pn(xn,yn)在双曲线 上(n,xn,yn都是正整数,且x1<x2<x3<…<xn).抛物线y=ax2+bx+c经过(0,3),(-2,3),(1,0)三点.
上(n,xn,yn都是正整数,且x1<x2<x3<…<xn).抛物线y=ax2+bx+c经过(0,3),(-2,3),(1,0)三点.
| x | … | … | |||||
| y | … | … |
(2)直接写出点pn(xn,yn)的坐标,并写出pn中任意两点所确定的不同直线的条数;
(3)从(2)中得到的所有直线中随机(任意)取出一条,利用图象求取出的直线与抛物线有公共点的概率;
(4)设抛物线y=ax2+bx+c与x轴的交点分别为A,B(A在B左侧),将抛物线y=ax2+bx+c向上平移,平移后的抛物线与x轴的交点分别记为C,D(C在D左侧),求
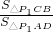 值.
值.
如图,平面直角坐标系xOy中,点pn(xn,yn)在双曲线 上(n,xn,yn都是正整数,且x1<x2<x3<…<xn).抛物线y=ax2+bx+c经过(0,3),(-2,3),(1,0)三点.
上(n,xn,yn都是正整数,且x1<x2<x3<…<xn).抛物线y=ax2+bx+c经过(0,3),(-2,3),(1,0)三点.
(1)求抛物线y=ax2+bx+c的解析式并在坐标系中画出它的图象;
(2)直接写出点pn(xn,yn)的坐标,并写出pn中任意两点所确定的不同直线的条数;
(3)从(2)中得到的所有直线中随机(任意)取出一条,利用图象求取出的直线与抛物线有公共点的概率;
(4)设抛物线y=ax2+bx+c与x轴的交点分别为A,B(A在B左侧),将抛物线y=ax2+bx+c向上平移,平移后的抛物线与x轴的交点分别记为C,D(C在D左侧),求 值.
值.

 上(n,xn,yn都是正整数,且x1<x2<x3<…<xn).抛物线y=ax2+bx+c经过(0,3),(-2,3),(1,0)三点.
上(n,xn,yn都是正整数,且x1<x2<x3<…<xn).抛物线y=ax2+bx+c经过(0,3),(-2,3),(1,0)三点. | x | … | … | |||||
| y | … | … |
(2)直接写出点pn(xn,yn)的坐标,并写出pn中任意两点所确定的不同直线的条数;
(3)从(2)中得到的所有直线中随机(任意)取出一条,利用图象求取出的直线与抛物线有公共点的概率;
(4)设抛物线y=ax2+bx+c与x轴的交点分别为A,B(A在B左侧),将抛物线y=ax2+bx+c向上平移,平移后的抛物线与x轴的交点分别记为C,D(C在D左侧),求
 值.
值.

 已知函数y=
已知函数y= (2011•西城区模拟)如图,平面直角坐标系xOy中,点pn(xn,yn)在双曲线
(2011•西城区模拟)如图,平面直角坐标系xOy中,点pn(xn,yn)在双曲线 已知函数y=
已知函数y=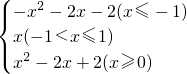 ,请充分利用探究函数图象性质的经验画出此函数的图象并写出两条关于此函数的性质.(不必列表、求点的坐标,直接在图中画图象)
,请充分利用探究函数图象性质的经验画出此函数的图象并写出两条关于此函数的性质.(不必列表、求点的坐标,直接在图中画图象)