题目内容
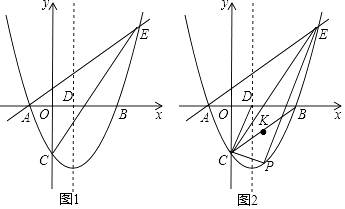
【题目】抛物线y=ax2+c与x轴交于A,B两点,顶点为C,点P为抛物线上,且位于x轴下方.
(1)如图1,若P(1,﹣3),B(4,0).
①求该抛物线的解析式;
②若D是抛物线上一点,满足∠DPO=∠POB,求点D的坐标;
(2)如图2,已知直线PA,PB与y轴分别交于E、F两点.当点P运动时, ![]() 是否为定值?若是,试求出该定值;若不是,请说明理由.
是否为定值?若是,试求出该定值;若不是,请说明理由.
【答案】
(1)
解:①将P(1,﹣3),B(4,0)代入y=ax2+c,得
![]() ,解得
,解得 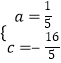 ,
,
抛物线的解析式为y= ![]() x2﹣
x2﹣ ![]() ;
;
②如图1
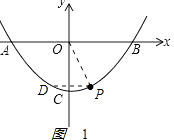 ,
,
由∠DPO=∠POB,得
DP∥OB,
D与P关于y轴对称,P(1,﹣3),
得D(﹣1,﹣3);
(2)
解:点P运动时, ![]() 是定值,
是定值,
设P点坐标为(m, ![]() m2﹣
m2﹣ ![]() ),A(﹣4,0),B(4,0),
),A(﹣4,0),B(4,0),
设AP的解析式为y=kx+b,将A、P点坐标代入,得
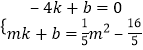 ,
,
解得b= ![]() ,即E(0,
,即E(0, ![]() ),
),
设BP的解析式为y=k1x+b1,将B、P点坐标代入,得
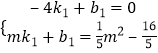 ,
,
解得b2= ![]() ,即F(0,
,即F(0, ![]() ),
),
OF+OE= ![]() +
+ ![]() =
= ![]() =
= ![]() ,
,
![]() =
= ![]() =2.
=2.
【解析】本题考查了二次函数综合题,①利用待定系数法求函数解析式;②利用函数值相等的点关于对称轴对称得出D点坐标是解题关键;(2)利用待定系数法求出E、F点坐标是解题关键.(1)①根据待定系数法求函数解析式,可得答案;②根据平行线的判定,可得PD∥OB,根据函数值相等两点关于对称轴对称,可得D点坐标;(2)根据待定系数法,可得E、F点的坐标,根据分式的性质,可得答案.

【题目】小青在本学期的数学成绩如下表所示(成绩均取整数):
测验类别 | 平时 | 期中考试 | 期末考试 | |||
测验1 | 测验1 | 测验1 | 课题学习 | |||
成绩 | 88 | 70 | 96 | 86 | 85 |
|

(1)计算小青本学期的平时平均成绩;
(2)如果学期的总评成绩是根据图所示的权重计算,那么本学期小青的期末考试成绩x至少为多少分才能保证达到总评成绩90分的最低目标?