题目内容
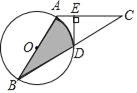
【题目】如图,AB是⊙O的直径,弦CD⊥AB,过点C作⊙O的切线与AB的延长线交于点P.若∠BCD=32°,则∠CPD的度数是( )

A. 64° B. 62° C. 58° D. 52°
【答案】D
【解析】
连接OC,根据三角形的内角和得到∠OBC=58°,根据等腰三角形的性质得到∠OCB=∠OBC=58°,根据切线的性质得到∠OCP=90°,得到∠CPO=26°,根据线段垂直平分线的性质得到PC=PD,于是得到结论.
解:连接OC,
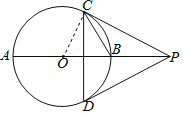
∵CD⊥AB,∠BCD=32°,
∴∠OBC=58°,
∵OC=OB,
∴∠OCB=∠OBC=58°,
∴∠COP=64°,
∵PC是⊙O的切线,
∴∠OCP=90°,
∴∠CPO=26°,
∵AB⊥CD,
∴AB垂直平分CD,
∴PC=PD,
∴∠CPD=2∠CPO=52°,
故选:D.

练习册系列答案
相关题目