题目内容
以x为自变量的二次函数y=-x2+2x+m,它的图象与y轴交于点C(0,3),与x轴交于点A、B, 点A在点B的左边,点O为坐标原点,
点A在点B的左边,点O为坐标原点,(1)求这个二次函数的解析式及点A,点B的坐标,画出二次函数的图象;
(2)在x轴上是否存在点Q,在位于x轴上方部分的抛物线上是否存在点P,使得以A,P,Q三点为顶点的三角形与△AOC相似(不包含全等)?若存在,请求出点P,点Q的坐标;若不存在,请说明理由.
分析:(1)根据C点坐标,可确定m的值,从而得到抛物线的解析式,令函数解析式的y=0,即可求得A、B的坐标.
(2)根据函数图象可知,显然∠PAQ不能是直角,已知以A,P,Q三点为顶点的三角形与△AOC相似但不全等,因此P、C不重合,即∠PAQ≠∠CAO,所以只考虑∠PAQ=∠ACO的情况,过A作∠PAQ=∠ACQ,交抛物线于点P,然后分两种情况:
①∠PQA=∠COA=90°,此时PQ⊥x轴,可设出点Q的坐标,根据抛物线的解析式可表示出点P的坐标,进而根据相似三角形的比例线段求出点Q、P的坐标;
②∠APQ=∠COA=90°,设出点Q的坐标,然后表示出PA的长,根据相似三角形的比例线段即可求出此时点Q的坐标.
(2)根据函数图象可知,显然∠PAQ不能是直角,已知以A,P,Q三点为顶点的三角形与△AOC相似但不全等,因此P、C不重合,即∠PAQ≠∠CAO,所以只考虑∠PAQ=∠ACO的情况,过A作∠PAQ=∠ACQ,交抛物线于点P,然后分两种情况:
①∠PQA=∠COA=90°,此时PQ⊥x轴,可设出点Q的坐标,根据抛物线的解析式可表示出点P的坐标,进而根据相似三角形的比例线段求出点Q、P的坐标;
②∠APQ=∠COA=90°,设出点Q的坐标,然后表示出PA的长,根据相似三角形的比例线段即可求出此时点Q的坐标.
解答:解:(1)根据题意,把点C(0,3)代入y=-x2+2x+m,
解得m=3,
即二次根式的解析式为y=-x2+2x+3,
即-x2+2x+3=0,
解得x1=-1,x2=3,
∴点A,点B的坐标分别是(-1,0),(3,0).
(2)假设存在符合题意的点P、Q,一定是∠PAQ=∠ACO;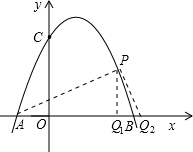
∵若PAQ=∠CAO,则点P与点C重合,
点Q与点O重合,
∴△PAQ≌△CAO,不合题意;
∵若∠PAQ=∠COA=90°,显然P不在抛物线上,
过A作AP,使∠PAO=∠ACO且与抛物线交于点P,
①若过点P作PQ1⊥x轴交x轴于Q1点,
设Q1(x1,0),P(x1,y1),
∵∠CQ1A=∠AOC,则△PQ1A∽△AOC,
∴
=
,
即
=-x12+2x1+3,
解得x1=
,代入抛物线的解析式中,
得y1=
,
∴Q1(
,0),P(
,
),存在△PQ1A∽△AOC;
②由①所得点P作PQ2⊥AP交x轴于Q2,
设Q2(x2,0);
∵∠APQ2∠COA,则△Q2PA∽△AOC,
∴
=
,
=
,x2=
.
∴Q2(
,0),存在△PQ2A∽△AOC;
综上所述,存在符合条件的相似三角形,且Q、P的坐标为:Q1(
,0),Q2(
,0),P(
,
).
解得m=3,
即二次根式的解析式为y=-x2+2x+3,
即-x2+2x+3=0,
解得x1=-1,x2=3,
∴点A,点B的坐标分别是(-1,0),(3,0).
(2)假设存在符合题意的点P、Q,一定是∠PAQ=∠ACO;

∵若PAQ=∠CAO,则点P与点C重合,
点Q与点O重合,
∴△PAQ≌△CAO,不合题意;
∵若∠PAQ=∠COA=90°,显然P不在抛物线上,
过A作AP,使∠PAO=∠ACO且与抛物线交于点P,
①若过点P作PQ1⊥x轴交x轴于Q1点,
设Q1(x1,0),P(x1,y1),
∵∠CQ1A=∠AOC,则△PQ1A∽△AOC,
∴
| AQ1 |
| OC |
| Q1P |
| AO |
即
| x1+1 |
| 3 |
解得x1=
| 8 |
| 3 |
得y1=
| 11 |
| 9 |
∴Q1(
| 8 |
| 3 |
| 8 |
| 3 |
| 11 |
| 9 |
②由①所得点P作PQ2⊥AP交x轴于Q2,
设Q2(x2,0);
∵∠APQ2∠COA,则△Q2PA∽△AOC,
∴
| AQ2 |
| CA |
| PA |
| OC |
| x2+1 | ||
|
| ||||||
| 3 |
| 83 |
| 27 |
∴Q2(
| 83 |
| 27 |
综上所述,存在符合条件的相似三角形,且Q、P的坐标为:Q1(
| 8 |
| 3 |
| 83 |
| 27 |
| 8 |
| 3 |
| 11 |
| 9 |
点评:此题考查了二次函数解析式的确定、函数图象与坐标轴交点坐标的求法、相似三角形的判定和性质等知识.(3)题中,应根据相似三角形的不同对应顶点分类讨论,这是此题的难点.

练习册系列答案
相关题目