题目内容
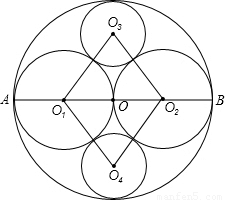
已知大⊙O的直径AB=acm,分别以OA、OB为直径作⊙O1和⊙O2,并在⊙O与⊙O1和⊙O2的空隙间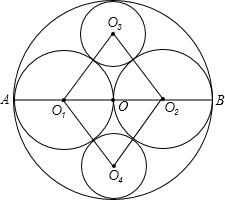 作两个半径都为r的⊙O3和⊙O4,且这些圆互相内切或外切(如图所示).
作两个半径都为r的⊙O3和⊙O4,且这些圆互相内切或外切(如图所示).(1)猜想四边形O1O4O2O3是什么四边形,并说明理由;
(2)求四边形O1O4O2O3的面积.
分析:(1)根据外切两圆之间之间的关系:圆心距等于两圆半径的和,即可证得四边形的四边相等;
(2)连接O3O4必过点O,且O3O4⊥AB,则菱形被分成了四个全等的直角三角形,根据菱形的面积公式即可求解.
(2)连接O3O4必过点O,且O3O4⊥AB,则菱形被分成了四个全等的直角三角形,根据菱形的面积公式即可求解.
解答:解:(1)四边形O1O4O2O3为菱形.(1分)
理由如下:
∵⊙O、⊙O1、⊙O2、⊙O3、⊙O4互相内切或外切,
又∵⊙O1和⊙O2,⊙O3和⊙O4分别是等圆,
∴O1O4=O4O2=O2O3=O3O1=
+r.(2分)
∴四边形O1O4O2O3为菱形.(3分)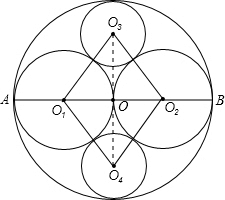
(2)连接O3O4必过点O,且O3O4⊥AB.(4分)
∵⊙O3和⊙O4的半径为rcm.
又∵⊙O1、⊙O2的半径为
cm,
∴在Rt△O3O1O中,有(
)2+(
-r)2=(
+r)2.
解得r=
.(6分)
∴O3O=
-
=
.
∵四边形O1O4O2O3为菱形,
∴S四边形O1O4O2O3=
•
=
.(8分)
理由如下:
∵⊙O、⊙O1、⊙O2、⊙O3、⊙O4互相内切或外切,
又∵⊙O1和⊙O2,⊙O3和⊙O4分别是等圆,
∴O1O4=O4O2=O2O3=O3O1=
| a |
| 4 |
∴四边形O1O4O2O3为菱形.(3分)

(2)连接O3O4必过点O,且O3O4⊥AB.(4分)
∵⊙O3和⊙O4的半径为rcm.
又∵⊙O1、⊙O2的半径为
| a |
| 4 |
∴在Rt△O3O1O中,有(
| a |
| 4 |
| a |
| 2 |
| a |
| 4 |
解得r=
| a |
| 6 |
∴O3O=
| a |
| 2 |
| a |
| 6 |
| a |
| 3 |
∵四边形O1O4O2O3为菱形,
∴S四边形O1O4O2O3=
| a |
| 2 |
| a |
| 3 |
| a2 |
| 6 |
点评:本题主要考查了两圆外切时的关系以及菱形的判定,菱形的计算可以通过作对角线分成四个全等的直角三角形进行计算.

练习册系列答案
相关题目

 作两个半径都为r的⊙O3和⊙O4,且这些圆互相内切或外切(如图所示).
作两个半径都为r的⊙O3和⊙O4,且这些圆互相内切或外切(如图所示).