题目内容
平行四边形的四个内角平分线能够围成（ ）A．平行四边形
B．菱形
C．矩形
D．正方形
【答案】分析：先作出草图，根据平行四边形的邻角互补，又是四个角的平分线，所以可以求出∠AEB=90°，同理可以求出四边形EFGH的其它三个内角都是直角，然后根据有三个角都是直角的四边形是矩形即可判定．
解答：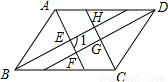
解：如图，在平行四边形ABCD中，∠ABC+∠BAD=180°，
∵AE平分∠BAD，BE平分∠ABC，
∴∠BAE+∠ABE=
（∠BAD+∠ABC）=
×180°=90°，
∴∠AEB=180°-90°=90°，
∴∠1=∠AEB=90°（对顶角相等），
同理∠EFG=∠FGH=∠GHE=90°，
∴四边形EFGH是矩形．
故选C．
点评：本题考查了平行四边形邻角互补的性质，角平分线的定义，有三个角是直角的四边形是矩形的判定定理，熟练掌握定理是解题的关键．
解答：
解：如图，在平行四边形ABCD中，∠ABC+∠BAD=180°，∵AE平分∠BAD，BE平分∠ABC，
∴∠BAE+∠ABE=
（∠BAD+∠ABC）=×180°=90°，∴∠AEB=180°-90°=90°，
∴∠1=∠AEB=90°（对顶角相等），
同理∠EFG=∠FGH=∠GHE=90°，
∴四边形EFGH是矩形．
故选C．
点评：本题考查了平行四边形邻角互补的性质，角平分线的定义，有三个角是直角的四边形是矩形的判定定理，熟练掌握定理是解题的关键．
练习册系列答案
口算题天天练系列答案
相关题目