题目内容
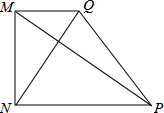 如图,直角梯形MNPQ,∠MNP=90°,PM⊥NQ,若
如图,直角梯形MNPQ,∠MNP=90°,PM⊥NQ,若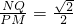 ,则
,则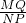 =
=
- A.

- B.

- C.4
- D.

A
分析:首先设PM与NQ相较于点O,由直角梯形MNPQ,∠MNP=90°,PM⊥NQ,易证得△MNQ∽△NPM,然后由相似三角形的对应边成比例,求得答案.
解答: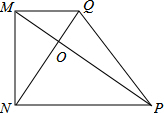 解:设PM与NQ相较于点O,
解:设PM与NQ相较于点O,
∵PM⊥NQ,
∴∠QMO+∠MQO=90°,
∵直角梯形MNPQ,∠MNP=90°,
∴∠MNQ+∠MQO=90°,MQ∥PN,∠MNP=∠MNP=90°,
∴∠MPN=∠QMO,
∴∠MPN=∠MNQ,
∴△MNQ∽△NPM,
∴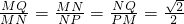 ,
,
∴MQ= ,NP=
,NP= MN,
MN,
∴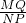 =
= .
.
故选A.
点评:此题考查了相似三角形的判定与性质、梯形的性质以及直角三角形的性质.此题难度适中,注意掌握数形结合思想的应用.
分析:首先设PM与NQ相较于点O,由直角梯形MNPQ,∠MNP=90°,PM⊥NQ,易证得△MNQ∽△NPM,然后由相似三角形的对应边成比例,求得答案.
解答:
 解:设PM与NQ相较于点O,
解:设PM与NQ相较于点O,∵PM⊥NQ,
∴∠QMO+∠MQO=90°,
∵直角梯形MNPQ,∠MNP=90°,
∴∠MNQ+∠MQO=90°,MQ∥PN,∠MNP=∠MNP=90°,
∴∠MPN=∠QMO,
∴∠MPN=∠MNQ,
∴△MNQ∽△NPM,
∴
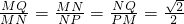 ,
,∴MQ=
 ,NP=
,NP= MN,
MN,∴
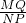 =
= .
.故选A.
点评:此题考查了相似三角形的判定与性质、梯形的性质以及直角三角形的性质.此题难度适中,注意掌握数形结合思想的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目