题目内容
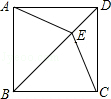
【题目】如图,在矩形ABCD中,AD>AB,AE是∠BAC的平分线交BC于点E,以AC上一点O 为圆心作圆,使 ⊙O经过A,E两点,⊙O交AC于点F,
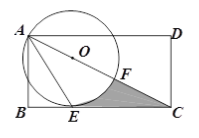
(1)求证:BC是⊙O的切线;
(2)若AB=3,∠BAC=60°,试求图中阴影部分的面积.
【答案】(1)证明见解析(2)![]()
【解析】试题分析:(1)连接OE,根据平行线判定推出OE∥AC,推出OE⊥BC,根据切线的判定推出即可;
(2)求出AE,OE,CE,利用S阴影=SΔOEC-S扇形EOF求出即可.
试题解析:(1)如图,连接OE,
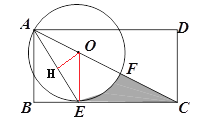
∵OA=OE,
∴∠OAE=∠OEA,
∵AE平分∠BAC,
∴∠BAE=∠CAE,
∴∠OEA=∠CAE,
∴OE∥AC,
∵∠C=90°,
∴∠OEC=90°,
∴OE⊥BC,
∵OE为半径,
∴BC是⊙O切线;
(2)根据题意得:∠BAE=30°.
∴cos30°=![]() ,即:AE=
,即:AE=![]()
过点O作OH⊥AE,垂足为F,可求得OE=2,∠COE=60°
∴![]()
∴CE=OEtan60°=![]()
∴S阴影=SΔOEC-S扇形EOF= ![]()

【题目】中华文明,源远流长:中华汉字,寓意深广,为了传承优秀传统文化,某校团委组织了一次全校3000名学生参加的“汉字听写”大赛,赛后发现所有参赛学生的成绩均不低于50分.为了更好地了解本次大赛的成绩分布情况,随机抽取了其中200名学生的成绩(成绩x取整数,总分100分)作为样本进行整理,得到下列不完整的统计图表:
成绩x/分 | 频数 | 频率 |
50≤x<60 | 10 | 0.05 |
60≤x<70 | 20 | 0.10 |
70≤x<80 | 30 | b |
80≤x<90 | a | 0.30 |
90≤x≤100 | 80 | 0.40 |
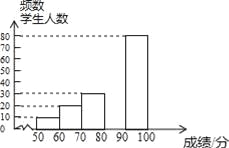
请根据所给信息,解答下列问题:
(1)a=______,b=______;
(2)请补全频数分布直方图;
(3)这次比赛成绩的中位数会落在_____________分数段;
(4)若成绩在90分以上(包括90分)的为“优”等,则该校参加这次比赛的3000名学生中成绩“优”等约有多少人?
【题目】如图所示的日历中,任意圈出一竖列相邻的三个数,设中间一个数为a,则这三个数之和为(用含a的式子表示)
日 | 一 | 二 | 三 | 四 | 五 | 六 |
1 | 2 | 3 | 4 | |||
5 | 6 | 7 | 8 | 9 | 10 | 11 |
12 | 13 | 14 | 15 | 16 | 17 | 18 |
19 | 20 | 21 | 22 | 23 | 24 | 25 |
26 | 27 | 28 | 29 | 30 | 31 |