��Ŀ����
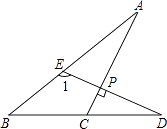
����Ŀ��С���Ͱְ���ĩ��ʪ�ع����ж�������������9��00�ӹ���ڳ���������ͬ·�������˶���С��15���Ӻ�Ŀ�ĵأ���ʱ�ְ־������1200�ף�С������Ŀ�ĵغ�������ԭ·���ٷ��أ���ְ������Ͱְ�һ���ԭ·���س����أ�С�����ְ��ڶ���������������ص�·����С��������ʱ��ĺ�����ϵ��ͼ��
��1��ͼ��![]() �� ����
�� ���� ![]() �� ����
�� ����
��2����С���Ͱְ�������ʱ�䣮
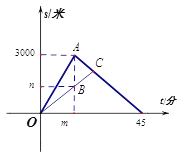
���𰸡���1��15��1200����2��9��25
�����������������1���������⣬���ͼ����жϳ�С������ɽ����ʱ���Լ��ְ־���ɽ���µ�·�̣���2����ͼ����Եó��ְ���ɽ���ٶȺ�С����ɽ���ٶȣ��������С������ɽ����ְ������õ�ʱ��.
��������� ��1����ͼ����Կ���ͼ��![]() .
.
��2���裺С���ӷ��̵���ְ���������x����
��ͼ����Եó��ְ���С������ǰ���ٶ��ǣ�1200��15=80��/�֣�С�����̵��ٶ��ǣ�3000�£�45��15��=100��/�֣�
80x+100x=1800
��x=10����
��С���ӳ�������ְ�����������15+10������
��С���Ͱְ�������ʱ����9��25.

����Ŀ����ͼ��ʾ������������a��b��c��d�ĸ�ͼ��ͼ�γ���ƽ��ͼ�����䶥������������������֮�����ij�ֹ�ϵ���۲�ͼb�ͱ��ж�Ӧ����ֵ��̽�������ķ���������

��1����һ��ÿ��ͼ�и��ж��ٸ����㡢�������ߣ���Щ��Χ�����ٸ����������
ƽ��ͼ | a | b | c | d |
������(S) | 7 | |||
����(M) | 9 | |||
������(N) | 3 |
��2�����ݱ�����ֵ��д��ƽ��ͼ�Ķ�������������������֮���һ�ֹ�ϵΪ ��
��3�����һ��ƽ��ͼ��20�������11��������ô���ã�2���еó��Ĺ�ϵ��֪���ƽ��ͼ�� ���ߣ�
����Ŀ�����ݺͺ���ij��ͬʱ����ij���ͺŵĻ�������̨�����ݳ���֧Ԯ���![]() ̨�����ݳ���֧Ԯ���
̨�����ݳ���֧Ԯ���![]() ̨�����ھ������人
̨�����ھ������人![]() ̨���ϲ�
̨���ϲ�![]() ̨��ÿ̨�������˷ѣ���λ����Ԫ��������躼�������ϲ��Ļ���Ϊ
̨��ÿ̨�������˷ѣ���λ����Ԫ��������躼�������ϲ��Ļ���Ϊ![]() ̨��
̨��
�ϲ� | �人 | |
���ݳ� |
|
|
���ݳ� |
|
|
��![]() ����
����![]() �Ĵ���ʽ����ʾ���˷ѣ���λ����Ԫ����
�Ĵ���ʽ����ʾ���˷ѣ���λ����Ԫ����
��![]() �������˷�Ϊ
�������˷�Ϊ![]() Ԫ�����������ϲ��Ļ���ӦΪ����̨?
Ԫ�����������ϲ��Ļ���ӦΪ����̨?
��![]() ������������ʹ���˷���
������������ʹ���˷���![]() Ԫ?���п��ܣ���д����Ӧ�ĵ��˷����������ܣ���˵�����ɣ�
Ԫ?���п��ܣ���д����Ӧ�ĵ��˷����������ܣ���˵�����ɣ�