题目内容
已知正方形纸片 的边长为2.操作:如图1,将正方形纸片折叠,使顶点
的边长为2.操作:如图1,将正方形纸片折叠,使顶点![]() 落在边
落在边![]() 上的点
上的点![]() 处(点
处(点![]() 与
与![]() 、
、![]() 不重合),折痕为
不重合),折痕为![]() ,折叠后
,折叠后![]() 边落在
边落在![]() 的位置,
的位置,![]() 与
与![]() 交于点
交于点![]() .
.
探究:1.观察操作结果,找到一个与![]() 相似的三角形,并证明你的结论;
相似的三角形,并证明你的结论;
2.当点![]() 位于
位于![]() 中点时,你找到的三角形与
中点时,你找到的三角形与![]() 周长的比是多少(图2为备用图)?
周长的比是多少(图2为备用图)?
1.与![]() 相似的三角形是
相似的三角形是![]() .
.
证明:∵四边形![]() 是正方形,
是正方形,
∴∠![]() =∠
=∠![]() =∠
=∠![]() =
=![]()
由折叠知 ∠![]() =∠
=∠![]() =
=![]() .
.
∴∠![]() +∠
+∠![]() =
=![]() ,∠
,∠![]() +∠
+∠![]() =
=![]() .
.
∴∠![]() =∠
=∠![]() .
.
∴![]() ∽
∽![]() .
.
2.设![]() =x,则
=x,则![]() =
=![]() ,
,
由折叠可知:![]() =
=![]() .
.
∵点![]() 是
是![]() 中点,
中点,
∴![]() =1.
=1.
∵∠![]() =
=![]() ,
,
∴![]() .
.
即![]() .
.
解得 ![]() .
.
∴![]() .
.
∵![]() ∽
∽![]()
∴ .
.
∴![]() 与
与![]() 周长的比为4∶3.
周长的比为4∶3.
解析:略

练习册系列答案
相关题目
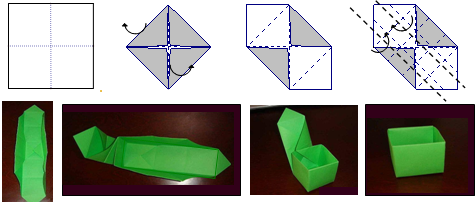









 的边长为2.操作:如图1,将正方形纸片折叠,使顶点
的边长为2.操作:如图1,将正方形纸片折叠,使顶点 落在边
落在边 上的点
上的点 处(点
处(点 、
、 不重合),折痕为
不重合),折痕为 ,折叠后
,折叠后 边落在
边落在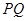 的位置,
的位置, 交于点
交于点 .
. 相似的三角形,并证明你的结论;
相似的三角形,并证明你的结论;