题目内容
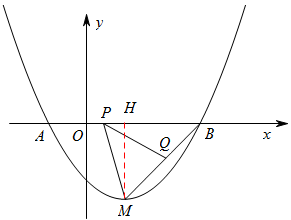
如图,抛物线 经过点
经过点 ,且与
,且与 轴交于点
轴交于点 、点
、点 ,若
,若 .
.
(1)求此抛物线的解析式;
(2)若抛物线的顶点为 ,点
,点 是线段
是线段 上一动点(不与点
上一动点(不与点 重合),
重合), ,射线
,射线 与线段
与线段 交于点
交于点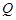 ,当△
,当△ 为等腰三角形时,求点
为等腰三角形时,求点 的坐标.
的坐标.
(1)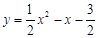 ;(2)
;(2)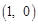 或
或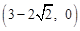 .
.
解析试题分析:(1)由 和
和 求出点
求出点 的坐标,从而根据曲线上点的坐标与方程的关系,列方程组求出
的坐标,从而根据曲线上点的坐标与方程的关系,列方程组求出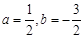 ,得到此抛物线的解析式.
,得到此抛物线的解析式.
(2)分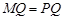 ,
,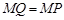 ,
,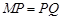 三种情况讨论即可.
三种情况讨论即可.
试题解析:(1)∵ ,∴
,∴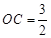 .
.
∵ ,∴
,∴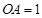 .∴
.∴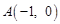 .
.
∵点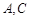 在抛物线
在抛物线 上,
上,
∴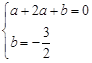 ,解得
,解得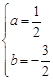 .
.
∴此抛物线的解析式为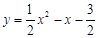 .
.
(2)∵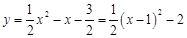 ,∴
,∴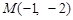 .
.
令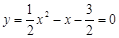 ,得
,得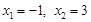 ,∴
,∴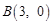 .
.
如图,作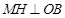 于点
于点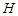 ,则
,则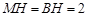 ,
,
∴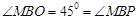 .
.
又∵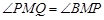 ,∴
,∴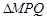 ∽
∽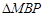 .
.
∴当△ 为等腰三角形时,
为等腰三角形时,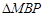 也为等腰三角形.
也为等腰三角形.
①当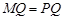 时,
时,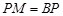 ,
,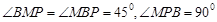 ,
,
∴点 与点
与点 重合,即
重合,即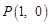 .
.
②当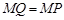 时,
时,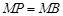 ,
,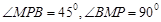 ,
,
∴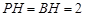 ,即
,即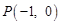 (舍去).
(舍去).
②当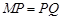 时,
时,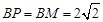 ,
,
∴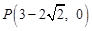 .
.
综上所述,当△ 为等腰三角形时,点
为等腰三角形时,点 的坐标为
的坐标为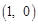 或
或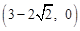 .
.
考点:1.锐角三角函数定义;2.曲线上点的坐标与方程的关系;3.二次函数的性质;4.等腰三角形的性质;5.分类思想的应用.

练习册系列答案
相关题目
 ,
, 求该抛物线与x轴的交点坐标;
求该抛物线与x轴的交点坐标; ,证明抛物线与x轴有两个交点;
,证明抛物线与x轴有两个交点; 且抛物线在
且抛物线在 区间上的最小值是-3,求b的值.
区间上的最小值是-3,求b的值. x2+
x2+ x(0≤x≤10).发射3 s后,导弹到达A点,此时位于与L同一水面的R处雷达站测得AR的距离是2 km,再过3 s后,导弹到达B点.
x(0≤x≤10).发射3 s后,导弹到达A点,此时位于与L同一水面的R处雷达站测得AR的距离是2 km,再过3 s后,导弹到达B点.

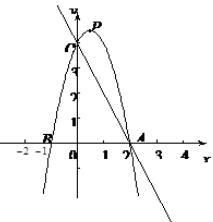
 x+m (m为常数)的图像与x轴交于点A(-3,0),与y轴交于点C.以直线x=1为对称轴的抛物线y=ax2+bx+c(a,b,c为常数,且a≠0)经过A、C两点,并与x轴的正半轴交于点B.
x+m (m为常数)的图像与x轴交于点A(-3,0),与y轴交于点C.以直线x=1为对称轴的抛物线y=ax2+bx+c(a,b,c为常数,且a≠0)经过A、C两点,并与x轴的正半轴交于点B.
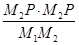 是否为定值,如果是,请直接写出结果,如果不是请说明理由.
是否为定值,如果是,请直接写出结果,如果不是请说明理由.
