��Ŀ����
��ƽ��ֱ������ϵ�У���P��������C��y=ax2�ڵ�һ�������ϵ�һ�㣬���� OP������O��OP�Ĵ��߽�����������һ��Q������PQ����y���ڵ�M��
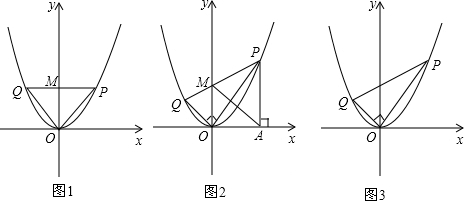
��1����ͼ1����PQ��x�ᣬ��PQ=2����������C�Ľ���ʽ��
��2����ͼ2������P��PA�Ax���ڵ�A�����P�ĺ�����Ϊm��
���ú�m�Ĵ���ʽ��ʾ��Q�ĺ�����Ϊ ��
������AM����֤��AM��OQ��
��3����ͼ3����������C��y=ax2������x�����ԳƱ任��Ȼ��ƽ�ƾ���P��Q����õ�������C�䣬��������C��Ķ���ΪR���ж��ı���OPRQ����״��

��1����ͼ1����PQ��x�ᣬ��PQ=2����������C�Ľ���ʽ��
��2����ͼ2������P��PA�Ax���ڵ�A�����P�ĺ�����Ϊm��
���ú�m�Ĵ���ʽ��ʾ��Q�ĺ�����Ϊ
������AM����֤��AM��OQ��
��3����ͼ3����������C��y=ax2������x�����ԳƱ任��Ȼ��ƽ�ƾ���P��Q����õ�������C�䣬��������C��Ķ���ΪR���ж��ı���OPRQ����״��
���㣺���κ����ۺ���
ר�⣺ѹ����
��������1�����ݶ��κ����ĶԳ��Կɵ�OP=OQ���Ӷ��õ���POQ�ǵ���ֱ�������Σ����ݵ���ֱ�������ε����������P�����꣬Ȼ����������߽���ʽ���a�����ɵý⣻
��2�����ݵ�P�ĺ��������OA��PA���ٹ���Q��QB��x����B�����Q�ĺ�����Ϊx����ʾ����Q�������꣬�ٸ��ݡ�AOP�͡�BQO���ƣ��������������ζ�Ӧ�߳ɱ�����ʽ��⼴�ɣ�
����ֱ��PQ�Ľ���ʽΪy=kx+b��k��0�������ô���ϵ�������ֱ�߽���ʽ���������M�����꣬Ȼ��������߶�Ӧ�ɱ������н���ȣ������������������BOQ�͡�OAM���ƣ��������������ζ�Ӧ����������BOQ=��OAM���ٸ���ͬλ����ȣ���ֱ��ƽ��֤�����ɣ�
��3������ͼ�Σ�Ȼ������ĸ��Ƕ���ֱ�ǵ��ı����Ǿ����жϼ��ɣ�
��2�����ݵ�P�ĺ��������OA��PA���ٹ���Q��QB��x����B�����Q�ĺ�����Ϊx����ʾ����Q�������꣬�ٸ��ݡ�AOP�͡�BQO���ƣ��������������ζ�Ӧ�߳ɱ�����ʽ��⼴�ɣ�
����ֱ��PQ�Ľ���ʽΪy=kx+b��k��0�������ô���ϵ�������ֱ�߽���ʽ���������M�����꣬Ȼ��������߶�Ӧ�ɱ������н���ȣ������������������BOQ�͡�OAM���ƣ��������������ζ�Ӧ����������BOQ=��OAM���ٸ���ͬλ����ȣ���ֱ��ƽ��֤�����ɣ�
��3������ͼ�Σ�Ȼ������ĸ��Ƕ���ֱ�ǵ��ı����Ǿ����жϼ��ɣ�
����⣺��1����PQ��x�ᣬ������y=ax2�ĶԳ���Ϊy�ᣬ
��OP=OQ��
��OP��OQ��
���POQ�ǵ���ֱ�������Σ�
��PQ=2��
��OM=MP=
��2=1��
���P��������1��1����
��a=1��
��������C�Ľ���ʽy=x2��
��2����ͼ2���ߵ�P�ĺ�����Ϊm��
��OA=m��PA=am2��
�ٹ���Q��QB��x����B�����Q�ĺ�����Ϊx�����Q��������Ϊy=ax2��
��OP��OQ�����AOP�ס�BQO��
��
=
��
��
=
��
���x=-
��
������Q�ĺ�����Ϊ-
��
�ʴ�Ϊ��-
��
����ֱ��PQ�Ľ���ʽΪy=kx+b��k��0����
��
��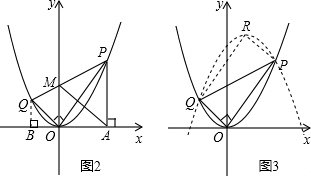
���
��
��ֱ��PQ�Ľ���ʽΪy=��am-
��x+
��
��x=0����y=
��
���M��0��
����
��
=
=am��
=
=am��
��
=
��
�֡ߡ�OBQ=��AOM=90�㣬
���BOQ�ס�OAM��
���BOQ=��OAM��
��AM��OQ��
��3����ͼ3���ɷ��ۺ�ƽ�Ƶ����ʣ���R=��POQ=90�㣬
��OQR=��OPR=��OPQ+��OQP=90�㣬
���ı���OPRQ�Ǿ��Σ�
��OP=OQ��
��OP��OQ��
���POQ�ǵ���ֱ�������Σ�
��PQ=2��
��OM=MP=
| 1 |
| 2 |
���P��������1��1����
��a=1��
��������C�Ľ���ʽy=x2��
��2����ͼ2���ߵ�P�ĺ�����Ϊm��
��OA=m��PA=am2��
�ٹ���Q��QB��x����B�����Q�ĺ�����Ϊx�����Q��������Ϊy=ax2��
��OP��OQ�����AOP�ס�BQO��
��
| OB |
| PA |
| BQ |
| OA |
��
| -x |
| am2 |
| ax2 |
| m |
���x=-
| 1 |
| a2m |
������Q�ĺ�����Ϊ-
| 1 |
| a2m |
�ʴ�Ϊ��-
| 1 |
| a2m |
����ֱ��PQ�Ľ���ʽΪy=kx+b��k��0����
��
|

���
|
��ֱ��PQ�Ľ���ʽΪy=��am-
| 1 |
| am |
| 1 |
| a |
��x=0����y=
| 1 |
| a |
���M��0��
| 1 |
| a |
��
| OA |
| OM |
| m | ||
|
| OB |
| BQ |
| ||
|
��
| OA |
| OM |
| OB |
| BQ |
�֡ߡ�OBQ=��AOM=90�㣬
���BOQ�ס�OAM��
���BOQ=��OAM��
��AM��OQ��
��3����ͼ3���ɷ��ۺ�ƽ�Ƶ����ʣ���R=��POQ=90�㣬
��OQR=��OPR=��OPQ+��OQP=90�㣬
���ı���OPRQ�Ǿ��Σ�
�����������Ƕ��κ����ۺ����ͣ���Ҫ�����˶��κ���ͼ�����Գ��ԣ�����ֱ�������ε��ж������ʣ�����ϵ��������κ�������ʽ�����������ε��ж������ʣ���2���������߹���������������ǽ���Ĺؼ�����3�����ݼ��α任����������ͼ�θ�����ֱ�ۣ�

��ϰ��ϵ�д�
 ͬ��ѧ��һ�ζ���ϵ�д�
ͬ��ѧ��һ�ζ���ϵ�д� �����ܾ�ϵ�д�
�����ܾ�ϵ�д� ���ƿ�����ϵ�д�
���ƿ�����ϵ�д� ���¿쳵����������ϵ�д�
���¿쳵����������ϵ�д�
�����Ŀ
ij�̵�ӪҵԱС��ÿ��������250Ԫ���ټ��ϸ���Ӫҵ���8%��Ϊ����һ�ܽ���ʱ��������378Ԫ����������з���ʽ��ʾ��s��ʾ���ܵ�Ӫҵ�250+0.08s=378����ô����ӪҵԱС�����۵�Ӫҵ���ǣ�������
| A��800Ԫ | B��1200Ԫ |
| C��1600Ԫ | D��2000Ԫ |
�±ߺ�����12������ÿ��������һ�����֣���֪�κ������������ֵĺͶ���20����x��ֵ�ǣ�������


| A��5 | B��10 | C��15 | D��20 |
������̣�a-b��x=|a-b|�Ľ���x=-1����ô��������
| A��a=b | B��a��b |
| C��a��b | D��a��b |
 ��ͼ����M��NΪ��ABC�ı�AC��BC�ϵ��������㣬�ó߹���AB������һ��P��ʹ
��ͼ����M��NΪ��ABC�ı�AC��BC�ϵ��������㣬�ó߹���AB������һ��P��ʹ