题目内容
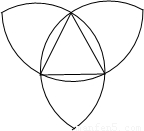
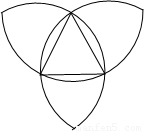
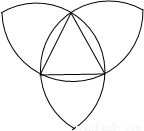
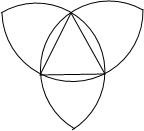已知一个等边三角形的边长为2，分别以它的三个顶点为圆心，边长为半径画弧，得到右图，那么图中所有的弧长的和是（ ）| A、4π | B、6π | C、8π | D、10π |
分析：根据弧长计算公式l=
，首先确定n与r的值，因为弧比较多可以分为9部分，此时n=60°，r=2，代入公式即可求出．
| nπr |
| 180 |
解答：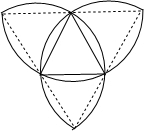
解：因为弧比较多可以分为9部分，如图所示
此时n=60°，r=2，代入公式得：
弧长计算公式l=
=
=
，
∴弧长的和是9×
=6π，
故答案为：6π．
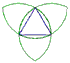
解：因为弧比较多可以分为9部分，如图所示此时n=60°，r=2，代入公式得：
弧长计算公式l=
| nπr |
| 180 |
| 60π×2 |
| 180 |
| 2π |
| 3 |
∴弧长的和是9×
| 2π |
| 3 |
故答案为：6π．
点评：此题主要考查了弧长的计算公式的应用，解决问题的关键是发现弧的特殊性，分解为9部分计算比较简单．
练习册系列答案
作业辅导系列答案
同步学典一课多练系列答案
经典密卷系列答案
金牌课堂练系列答案
相关题目
