题目内容
梯形上底长为L,中位线长为m,则连接两条对角线中点的线段长为( )
| A、m-2L | ||
B、
| ||
| C、2m-L | ||
| D、m-L |
分析:根据题意作出图形,根据三角形中位线定理和梯形中位线性质,通过等量关系代换可得到连接两条对角线中点的线段长.
解答: 解:根据题意作出如图,
解:根据题意作出如图,
梯形ABCD,AD平行BC,EF为中位线,与对角线交于GH,
∵中位线EF∥AD∥BC,
∴EG、HF为△BDA、△CAD的中位线,EH为△ABC的中位线,GF为△DBC的中位线,
∴EG=
AD,EH=
BC,HF=
AD,GF=
BC,EF=
(AD+BC)
即BC=2m-L,GH=EH-EG=GF-HF=
BC-
AD=
(BC-AD)=
(2m-L-L)=m-L.
故选D.
 解:根据题意作出如图,
解:根据题意作出如图,梯形ABCD,AD平行BC,EF为中位线,与对角线交于GH,
∵中位线EF∥AD∥BC,
∴EG、HF为△BDA、△CAD的中位线,EH为△ABC的中位线,GF为△DBC的中位线,
∴EG=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
即BC=2m-L,GH=EH-EG=GF-HF=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
故选D.
点评:本题考查了梯形中位线性质、三角形中位线定理,找到相应关系的线段是解题的关键,利用图形结合更能直观地得结论.

练习册系列答案
相关题目
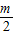 -L
-L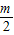 -L
-L