题目内容
(本题12分) 如图,在平面直角坐标系xoy中,矩形ABCD的边AB在x轴上,且AB=3,BC=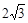 ,直线y=
,直线y=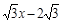 经过点C,交y轴于点G,且∠AGO=30°。
经过点C,交y轴于点G,且∠AGO=30°。
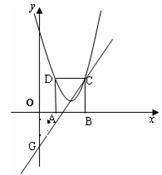
(1)点C、D的坐标分别是C( ),D( );
(2)求顶点在直线y=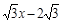 上且经过点C、D的抛物线的解析式;
上且经过点C、D的抛物线的解析式;
(3)将(2)中的抛物线沿直线y=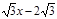 平移,平移后的抛物线交y轴于点F,顶点为点E。平移后是否存在这样的抛物线,使△EFG为等腰三角形?若存在,请求出此时抛物线的解析式;若不存在,请说明理由。
平移,平移后的抛物线交y轴于点F,顶点为点E。平移后是否存在这样的抛物线,使△EFG为等腰三角形?若存在,请求出此时抛物线的解析式;若不存在,请说明理由。
【答案】
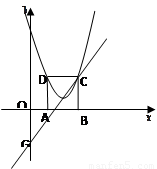 解:
解:
(1)C( 4,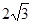 ),D(1,
),D(1,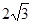 ); (4分)
); (4分)
(2)由抛物线的顶点坐标为(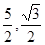 )(2分)可得抛物线的解析式为
)(2分)可得抛物线的解析式为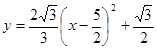 (2分)
(2分)
(3)设抛物线沿直线y=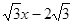 平移后的抛物线的顶点为
平移后的抛物线的顶点为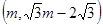 ,则平移后抛物线的解析式为
,则平移后抛物线的解析式为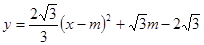
当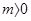 时,若
时,若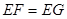 ,则
,则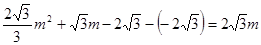
解得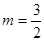
∴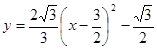
若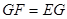 ,则
,则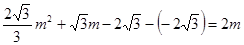
解得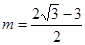
∴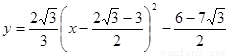
若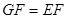 ,则∠
,则∠ 120°(不合题意,舍去)
120°(不合题意,舍去)
当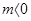 时,∠
时,∠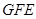 为钝角,则当⊿EFG为等腰三角形时,
为钝角,则当⊿EFG为等腰三角形时,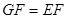
∴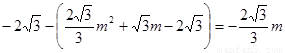
解得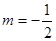 ,∴
,∴
【解析】略

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目




 x2+3与x轴交于点A、B,与直线y=
x2+3与x轴交于点A、B,与直线y=