题目内容
已知二次函数y=ax2+bx+c (a≠0)的图象如图所示,有下列5个结论:
①abc<0; ②b<a+c; ③4a+2b+c>0;④2c<3b;⑤a+b<m (am+b)(m≠1的实数),其中结论正确的个数有( )

A. 2个 B. 3个 C. 4个 D. 5个
练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
根据表中的二次函数y=ax2+bx+c的自变量x与函数y的对应值,可判断该二次函数的图象与x轴( )
x | … | ﹣1 | 0 | 1 | 2 | …[来 |
y | … | 4 | ﹣0.5 | ﹣2 | ﹣0.5 | … |
A. 只有一个交点
B. 有两个交点,且它们分别在y轴两侧
C. 有两个交点,且它们均在y轴同侧
D. 无交点
某企业信息部进行市场调研发现:
信息一:如果单独投资A种产品,所获利润yA(万元)与投资金额x(万元)之间存在某种关系的部分对应值如下表:
x(万元) | 1 | 2 | 2.5 | 3 | 5 |
yA(万元) | 0.4 | 0.8 | 1 | 1.2 | 2 |
信息二:如果单独投资B种产品,则所获利润yB(万元)与投资金额x(万元)之间存在二次函数关系:yB=ax2+bx,且投资2万元时获利润2.4万元,当投资4万元时,可获利润3.2万元.
(1)求出yB与x的函数关系式;
(2)从所学过的一次函数、二次函数、反比例函数中确定哪种函数能表示yA与x之间的关系,并求出yA与x的函数关系式;
(3)如果企业同时对A、B两种产品共投资15万元,请设计一个能获得最大利润的投资方案,并求出按此方案能获得的最大利润是多少?


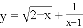 中自变量的取值范围是______________
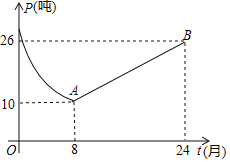
中自变量的取值范围是______________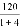 (0<t≤8)的图象与线段AB的组合;设第t个月销售该原料药每吨的毛利润为Q(单位:万元),Q与t之间满足如下关系:Q=
(0<t≤8)的图象与线段AB的组合;设第t个月销售该原料药每吨的毛利润为Q(单位:万元),Q与t之间满足如下关系:Q=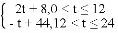
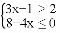 的解集在数轴上表示为( )
的解集在数轴上表示为( ) B.
B. 
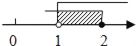 D.
D. 