Question

已知等边三角形的边长为

3

，则其内切圆半径为（　　）

• A、

  1

  2

• B、

  3

  2

• C、l
• D、

  3

Answer 1

分析：过O点作OD⊥AB，则AD=

3

2

，因为∠OAD=30°，根据直角三角形中的三角函数可求OD=tan30°•AD=

1

2

．

解答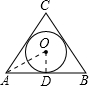：解：如图，过O点作OD⊥AB，则AD=

3

2

，
因为∠OAD=30°，
所以OD=tan30°•AD=

1

2

．
故选A．

点评：本题考查了三角形的内切圆与内心的计算．解这类题一般都利用过内心向正三角形的一边作垂线，则正三角形的半径、内切圆半径和正三角形边长的一半构成一个直角三角形，解这个直角三角形，可求出相关边长或角．