题目内容
某课题小组对课本的习题进行了如下探索,请逐步思考并解答:
(1)如图1,两个大小一样的传送轮连接着一条传送带,两个传动轮中心的距离是10m,求这条传送带的长
(2)改变图形的数量;
如图2、将传动轮增加到3个,每个传动轮的直径是3m,每两个传动轮中心的距离是10m,求这条传送带的长
(3)改变动态关系,将静态问题升华为动态问题:
如图3,一个半径为1cm的⊙P沿边长为2πcm的等边三角形△ABC的外沿作无滑动滚动一周,求圆心P经过的路径长?⊙P自转了多少周?
(4)拓展与应用
如图4,一个半径为1cm的⊙P沿半径为3cm的⊙O外沿作无滑动滚动一周,则⊙P自转了多少周?
(1)如图1,两个大小一样的传送轮连接着一条传送带,两个传动轮中心的距离是10m,求这条传送带的长
(20+3π)m
(20+3π)m
.(2)改变图形的数量;
如图2、将传动轮增加到3个,每个传动轮的直径是3m,每两个传动轮中心的距离是10m,求这条传送带的长
(30+3π)m
(30+3π)m
.(3)改变动态关系,将静态问题升华为动态问题:
如图3,一个半径为1cm的⊙P沿边长为2πcm的等边三角形△ABC的外沿作无滑动滚动一周,求圆心P经过的路径长?⊙P自转了多少周?
(4)拓展与应用
如图4,一个半径为1cm的⊙P沿半径为3cm的⊙O外沿作无滑动滚动一周,则⊙P自转了多少周?

分析:(1)利用弧长公式求出传送带等于中心的距离10×2+圆的周长即可;
(2)利用扇形弧长公式以及传送带组成分别求出即可;
(3)利用圆心P经过的路径长为“三角形的周长加一个半径为1的圆的周长”求出即可;
(4)利用⊙P的圆心P沿半径为3cm⊙O外沿作无滑动滚动一周的路径长为C=(3+1)×2π=8π,求出即可.
(2)利用扇形弧长公式以及传送带组成分别求出即可;
(3)利用圆心P经过的路径长为“三角形的周长加一个半径为1的圆的周长”求出即可;
(4)利用⊙P的圆心P沿半径为3cm⊙O外沿作无滑动滚动一周的路径长为C=(3+1)×2π=8π,求出即可.
解答: 解:(1)这条传送带的长为:20+2π×1.5=(20+3π)m,
解:(1)这条传送带的长为:20+2π×1.5=(20+3π)m,
(2)10+10+10+
π×1.5×3=(30+3π)m,
(3)如图3,圆心P经过的路径长为“三角形的周长加一个半径为1的圆的周长”
∴l=6π+2π=8π,
⊙P自转的周数=圆心P经过的路径长÷⊙P的周长,
∴⊙P自转的周数=8π÷2π=4,
(4)如图4,⊙P的圆心P沿半径为3cm⊙O外沿作无滑动滚动一周的路径长为C=(3+1)×2π=8π,
∴⊙P自转的圈数=8π÷2π=4.
 解:(1)这条传送带的长为:20+2π×1.5=(20+3π)m,
解:(1)这条传送带的长为:20+2π×1.5=(20+3π)m,(2)10+10+10+
| 120 |
| 180 |
(3)如图3,圆心P经过的路径长为“三角形的周长加一个半径为1的圆的周长”
∴l=6π+2π=8π,
⊙P自转的周数=圆心P经过的路径长÷⊙P的周长,
∴⊙P自转的周数=8π÷2π=4,
(4)如图4,⊙P的圆心P沿半径为3cm⊙O外沿作无滑动滚动一周的路径长为C=(3+1)×2π=8π,
∴⊙P自转的圈数=8π÷2π=4.
点评:此题主要考查了扇形的弧长公式以及等边三角形的性质,根据已知得出P经过路径是解题关键.

练习册系列答案
相关题目


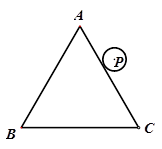








 3)改变动态关系,将静态问题升华为动态问题:
3)改变动态关系,将静态问题升华为动态问题:


