题目内容
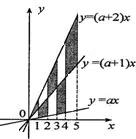 如图,在x轴上有五个点,它们的横坐标依次为1,2,3,4,5.分别过这些点作x轴的垂线与三条直线y=ax,y=(a+1)x,y=(a+2)x相交,其中a>0.若图中阴影部分的面积是75a,则a为
如图,在x轴上有五个点,它们的横坐标依次为1,2,3,4,5.分别过这些点作x轴的垂线与三条直线y=ax,y=(a+1)x,y=(a+2)x相交,其中a>0.若图中阴影部分的面积是75a,则a为分析:阴影部分由五个部分组成,分别为三角形或梯形,运用整体的思想,把阴影部分的五个部分组成一个三角形来求面积就简单多了.
解答:解:将8条直线共15个交点求出.(不计与坐标系的,很简单,直接写)
p1(1,a),p2(2,2a),p3(3,3a),p4 (4,4a),p5 (5,5a);
q1(1,(a+1)),…q5(5,5(a+1));
r1(1,(a+2))…r5(5,5(a+2)) (p1离原点最近,r5离原点最远)
用梯形公式求出各阴影部分面积并求和(底为纵坐标之差,高为1)
S1=
r1q1=
;
S2=
(q1p1+q2p2)×1=
;
S3=
((r2q2+r3q3)×1)
=
((2(a+2)-2(a+1))+(3(a+2)-3(a+1)))
=
,
同理可得S4=
,S5=
(仿S3一样计算)
∴S=S1+S2+S3+S4+S5=
+
+
+
+
=12.5,
∵S=75a,∴75a=12.5,
∴a=
.
故答案为
.
p1(1,a),p2(2,2a),p3(3,3a),p4 (4,4a),p5 (5,5a);
q1(1,(a+1)),…q5(5,5(a+1));
r1(1,(a+2))…r5(5,5(a+2)) (p1离原点最近,r5离原点最远)
用梯形公式求出各阴影部分面积并求和(底为纵坐标之差,高为1)
S1=
| 1 |
| 2 |
| 1 |
| 2 |
S2=
| 1 |
| 2 |
| 3 |
| 2 |
S3=
| 1 |
| 2 |
=
| 1 |
| 2 |
=
| 5 |
| 2 |
同理可得S4=
| 7 |
| 2 |
| 9 |
| 2 |
∴S=S1+S2+S3+S4+S5=
| 1 |
| 2 |
| 3 |
| 2 |
| 5 |
| 2 |
| 7 |
| 2 |
| 9 |
| 2 |
∵S=75a,∴75a=12.5,
∴a=
| 1 |
| 6 |
故答案为
| 1 |
| 6 |
点评:主要考查了反比例函数和三角形的面积公式,要会根据点的坐标求出所需要的线段的长度,灵活运用面积公式求解.
由于阴影部分是不规则的图形,且又分散在不同区域,故应该想到要运用整体思想将阴影部分集中在同一区域中求解.这样就比较自然地想到将分布在直线上方的三个阴影部分相应地转化到该直线下方的三个空白处.这样问题就转化为三角形面积的计算,经检验也确实符合如上所述的思考过程.本题以坐标系为考查载体,结合一次函数的图象将阴影部分的面积转化成三角形的面积来计算,比较鲜明地渗透了转化的思想与整体的思想,是一个思维含量较高的客观题.
由于阴影部分是不规则的图形,且又分散在不同区域,故应该想到要运用整体思想将阴影部分集中在同一区域中求解.这样就比较自然地想到将分布在直线上方的三个阴影部分相应地转化到该直线下方的三个空白处.这样问题就转化为三角形面积的计算,经检验也确实符合如上所述的思考过程.本题以坐标系为考查载体,结合一次函数的图象将阴影部分的面积转化成三角形的面积来计算,比较鲜明地渗透了转化的思想与整体的思想,是一个思维含量较高的客观题.

练习册系列答案
相关题目
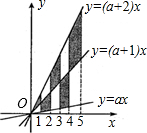 如图,在x轴上有五个点,它们的横坐标依次为1,2,3,4,5.分别过这些点作x轴的垂线与三条直线y=ax,y=(a+1)x,y=(a+2)x相交,其中a>0.则图中阴影部分的面积是( )
如图,在x轴上有五个点,它们的横坐标依次为1,2,3,4,5.分别过这些点作x轴的垂线与三条直线y=ax,y=(a+1)x,y=(a+2)x相交,其中a>0.则图中阴影部分的面积是( )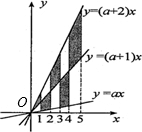 如图,在x轴上有五个点,它们的横坐标依次为1,2,3,4,5.分别过这些点作x轴的垂线与三条直线y=ax,y=(a+1)x,y=(a+2)x相交,其中a>0.则图中阴影部分的面积是
如图,在x轴上有五个点,它们的横坐标依次为1,2,3,4,5.分别过这些点作x轴的垂线与三条直线y=ax,y=(a+1)x,y=(a+2)x相交,其中a>0.则图中阴影部分的面积是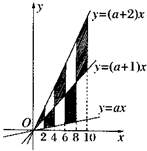 如图,在x轴上有五个点,它们的横坐标依次为2,4,6,8,10分别过这些点作x轴的垂线与三条直线y=ax,y=(a+1)x,y=(a+2)x相交,其中a>0,则图中阴影部分的面积是
如图,在x轴上有五个点,它们的横坐标依次为2,4,6,8,10分别过这些点作x轴的垂线与三条直线y=ax,y=(a+1)x,y=(a+2)x相交,其中a>0,则图中阴影部分的面积是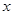 轴的垂线与三条直线
轴的垂线与三条直线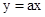 ,
,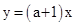 ,
,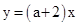 相交,其中
相交,其中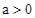 .则图中阴影部分的面积是( )
.则图中阴影部分的面积是( )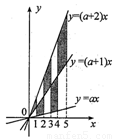
 D.25
D.25