题目内容
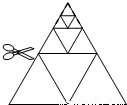
 如图,将一张正三角形纸片剪成四个小正三角形,得到4个小正三角形,称为第一次操作;然后,将其中的一个正三角形再剪成四个小正三角形,共得到7个小正三角形,称为第二次操作;再将其中的一个正三角形再剪成四个小正三角形,共得到10个小正三角形,称为第三次操作;…,根据以上操作,若要得到2011个小正三角形,则需要操作的次数是
如图,将一张正三角形纸片剪成四个小正三角形,得到4个小正三角形,称为第一次操作;然后,将其中的一个正三角形再剪成四个小正三角形,共得到7个小正三角形,称为第二次操作;再将其中的一个正三角形再剪成四个小正三角形,共得到10个小正三角形,称为第三次操作;…,根据以上操作,若要得到2011个小正三角形,则需要操作的次数是
- A.672
- B.671
- C.669
- D.670
D
分析:根据已知第一次操作后得到4个小正三角形,第二次操作后得到7个小正三角形;第三次操作后得到10个小正三角形;…继而即可求出剪m次时正三角形的个数为2011.
解答:∵第一次操作后得到4个小正三角形,第二次操作后得到7个小正三角形;第三次操作后得到10个小正三角形,
∴第m次操作后,总的正三角形的个数为3m+1.则:
2011=3m+1,
解得:m=670,
故若要得到2011个小正三角形,则需要操作的次数为670次.
故选:D.
点评:此题主要考查了图形的变化类,根据已知得出第m次操作后,总的正三角形的个数为3m+1是解题关键.
分析:根据已知第一次操作后得到4个小正三角形,第二次操作后得到7个小正三角形;第三次操作后得到10个小正三角形;…继而即可求出剪m次时正三角形的个数为2011.
解答:∵第一次操作后得到4个小正三角形,第二次操作后得到7个小正三角形;第三次操作后得到10个小正三角形,
∴第m次操作后,总的正三角形的个数为3m+1.则:
2011=3m+1,
解得:m=670,
故若要得到2011个小正三角形,则需要操作的次数为670次.
故选:D.
点评:此题主要考查了图形的变化类,根据已知得出第m次操作后,总的正三角形的个数为3m+1是解题关键.

练习册系列答案
相关题目
 (2011•沙坪坝区模拟)如图,将一张正三角形纸片剪成四个小正三角形,得到4个小正三角形,称为第一次操作;然后,将其中的一个正三角形再剪成四个小正三角形,共得到7个小正三角形,称为第二次操作;再将其中的一个正三角形再剪成四个小正三角形,共得到10个小正三角形,称为第三次操作;…,根据以上操作,若要得到2011个小正三角形,则需要操作的次数是( )
(2011•沙坪坝区模拟)如图,将一张正三角形纸片剪成四个小正三角形,得到4个小正三角形,称为第一次操作;然后,将其中的一个正三角形再剪成四个小正三角形,共得到7个小正三角形,称为第二次操作;再将其中的一个正三角形再剪成四个小正三角形,共得到10个小正三角形,称为第三次操作;…,根据以上操作,若要得到2011个小正三角形,则需要操作的次数是( )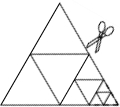 (2013•吴中区二模)如图,将一张正三角形纸片剪成四个小正三角形,得到4个小正三角形,称为第一次操作;然后,将其中的一个正三角形再剪成四个小正三角形,共得到7个小正三角形,称为第二次操作;再将其中的一个正三角形再剪成四个小正三角形,共得到10个小正三角形,称为第三次操作;…,根据以上操作,若要得到2014个小正三角形,则需要操作的次数是( )次.
(2013•吴中区二模)如图,将一张正三角形纸片剪成四个小正三角形,得到4个小正三角形,称为第一次操作;然后,将其中的一个正三角形再剪成四个小正三角形,共得到7个小正三角形,称为第二次操作;再将其中的一个正三角形再剪成四个小正三角形,共得到10个小正三角形,称为第三次操作;…,根据以上操作,若要得到2014个小正三角形,则需要操作的次数是( )次.