题目内容
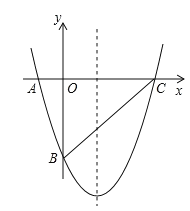
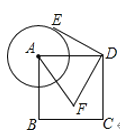
【题目】如图，已知正方形ABCD的边长为4，以点A为圆心，2为半径作圆，点E是⊙A上的任意一点，将点E绕点D按逆时针方向转转90°得到点F，连接AF、DF，则
的最小值是__．
【答案】5
【解析】
连接AE，CF，易证△ADE≌△CDF，所以CF=AE，可知F点在以C为圆心，2为半径的圆上运动，作出运动轨迹，在CD上截取CM=
CF=1，利用相似可得FM=DF，当A、F、M三点共线时，AM的长度即为
的最小值.
如图，连接AE，CF，
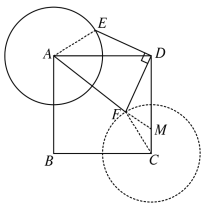
∵∠ADE+∠ADF=90°，∠ADF+∠CDF=90°，
∴∠ADE=∠CDF
在△ADE和△CDF中，
∴△ADE≌△CDF（SAS）
∴CF=AE，
∴F点在以C为圆心，2为半径的圆上运动，
如图所示，以C为圆心，2为半径作圆C，
在CD上截取CM=CF=1，
∵
，
，
∴
又∵∠FCM=∠DCF
∴△CMF∽△CFD
∴
，即
∴
当A、F、M三点共线时，AM的长度即为的最小值，
在Rt△ADM中，AD=4，DM=CD-CM=3，
∴
故答案为：5.
练习册系列答案
相关题目
【题目】有这样一个问题，探究函数y＝x2﹣2
的图象与性质，小张根据学习函数的经验，对函数y＝x2﹣2的图象与性质进行了研究，下面是小张的探究过程，请补充完整：
（1）函数y＝x2﹣2的自变量取值范围是 ．
（2）下表是y与x的几组对应值：
x | … | ﹣4 | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 4 | |
y | … | n | 3 | 0 | ﹣1 | 0 | ﹣1 | 0 | 3 | m |
求m的值；
（3）如图，在平面直角坐标系xOy中，算出了以上表中各对对应值为坐标的点，根据算出的点，画出该函数的图象；
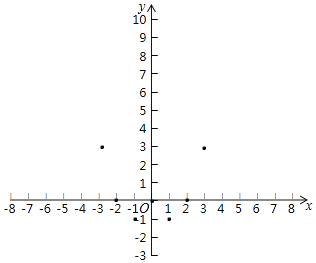
（4）进一步探究发现，该函数图象在第四象限内的最低点是1，﹣1），结合函数的图象，写出该函数的其他性质（一条即可）；
（5）根据图象回答：方程x2﹣2＝﹣
有 个实数解．
