题目内容
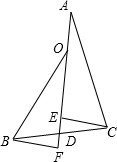如图，已知D为BC的中点，∠BOF=∠CAE，CE⊥AD，BF⊥AD，求证：AO=2DE．
证明：∵CE⊥AD，BF⊥AD，
∴CE∥BF，
又∵D是BC的中点，
∴DE=DF=
EF，CE=BF，
∵CE=BF，∠BOF=∠CAE，∠CEA=∠BFO=90°，
∴△BOF≌△CAE，
∴AE=OF，
∴AE-OE=OF-OE，
即AO=EF=2DE，
即AO=2DE．
分析：根据已知得出CE∥BF，推出DE=DF=EF，CE=BF，证△BOF≌△CAE，推出AE=OF，即可推出答案．
点评：本题主要考查对垂直的定义，全等三角形的性质和判定等知识点的理解和掌握，能求出DE=DF=EF和AE=OF是证此题的关键．
∴CE∥BF，
又∵D是BC的中点，
∴DE=DF=
EF，CE=BF，∵CE=BF，∠BOF=∠CAE，∠CEA=∠BFO=90°，
∴△BOF≌△CAE，
∴AE=OF，
∴AE-OE=OF-OE，
即AO=EF=2DE，
即AO=2DE．
分析：根据已知得出CE∥BF，推出DE=DF=
EF，CE=BF，证△BOF≌△CAE，推出AE=OF，即可推出答案．点评：本题主要考查对垂直的定义，全等三角形的性质和判定等知识点的理解和掌握，能求出DE=DF=
EF和AE=OF是证此题的关键． 
练习册系列答案
相关题目
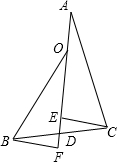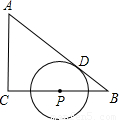
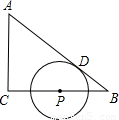
如图，已知D为BC的中点，∠BOF=∠CAE，CE⊥AD，BF⊥AD，求证：AO=2DE．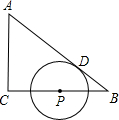
在Rt△ABC中，∠C=90°，AC=3，BC=4．
