题目内容
解关于x的不等式mx-2>3m+5x(m≠5).
解:移项得,mx-5x>3m+2
合并同类项得,(m-5)x>3m+2
(1)当m>5时,m-5>0,则
x>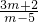 ;
;
(2)当m<5时,m-5<0,则
x<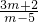 .
.
分析:根据解不等式的步骤,先移项、合并同类项,再根据m-1的符号讨论x的取值范围即可.
点评:本题考查了解简单不等式的能力,解答这类题学生往往在解题时不注意移项要改变符号这一点而出错.
解不等式要依据不等式的基本性质,在不等式的两边同时加上或减去同一个数或整式不等号的方向不变;在不等式的两边同时乘以或除以同一个正数不等号的方向不变;在不等式的两边同时乘以或除以同一个负数不等号的方向改变.
合并同类项得,(m-5)x>3m+2
(1)当m>5时,m-5>0,则
x>
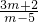 ;
;(2)当m<5时,m-5<0,则
x<
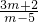 .
.分析:根据解不等式的步骤,先移项、合并同类项,再根据m-1的符号讨论x的取值范围即可.
点评:本题考查了解简单不等式的能力,解答这类题学生往往在解题时不注意移项要改变符号这一点而出错.
解不等式要依据不等式的基本性质,在不等式的两边同时加上或减去同一个数或整式不等号的方向不变;在不等式的两边同时乘以或除以同一个正数不等号的方向不变;在不等式的两边同时乘以或除以同一个负数不等号的方向改变.

练习册系列答案
相关题目