题目内容
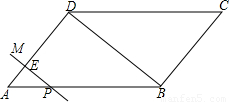
（2005•绵阳）如图，在△ABC中，∠C=90°，AC=8，AB=10，点P在AC上，AP=2，若⊙O的圆心在线段BP上，且⊙O与AB、AC都相切，则⊙O的半径是（ ）
A．1
B．
C．
D．
【答案】分析：设AC与⊙O相切于点D，连接OD，AO．在直角三角形ABC中，根据勾股定理，得BC=6，再证明BC=PC，所以可求∠BPC=45°．设⊙O的半径是r，根据三角形ABP的面积的两种表示方法，得2r+10r=12，解方程即可求解．
解答：
解：设AC与⊙O相切于点D，连接OD，AO，⊙O的半径是r，
∵∠C=90°，AC=8，AB=10，
∴BC=6，
∵PC=8-2=6，
∴BC=PC；
∴∠BPC=45°，
∴S△APB=S△APO+S△AOB=S△ABC-S△BCP，
×2r+
×10r=
×6×8-
×6×6
2r+10r=12，
解得r=1．
故选A．
点评：熟练运用勾股定理，根据已知条件发现特殊直角三角形，运用三角形面积的不同表示方法列方程求解．
解答：
解：设AC与⊙O相切于点D，连接OD，AO，⊙O的半径是r，∵∠C=90°，AC=8，AB=10，
∴BC=6，
∵PC=8-2=6，
∴BC=PC；
∴∠BPC=45°，
∴S△APB=S△APO+S△AOB=S△ABC-S△BCP，
×2r+×10r=×6×8-×6×62r+10r=12，
解得r=1．
故选A．
点评：熟练运用勾股定理，根据已知条件发现特殊直角三角形，运用三角形面积的不同表示方法列方程求解．
练习册系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
