��Ŀ����
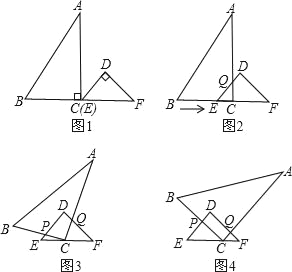
����Ŀ������ABC�У���ACB��45������D�����B��C���غϣ�Ϊ����BC��һ���㣬����AD����ADΪһ������AD���Ҳ���������ADEF��
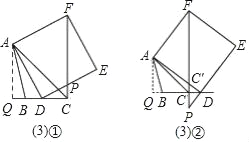
��1�����AB��AC����ͼ�٣��ҵ�D���߶�BC���˶������ж��߶�CF��BD֮���λ�ù�ϵ����֤����Ľ��ۣ�
��2�����AB��AC����ͼ�ڣ��ҵ�D���߶�BC���˶�����1���н����Ƿ������Ϊʲô��
��3����������ADEF�ı�DE����ֱ�����߶�CF����ֱ���ཻ�ڵ�P����AC��4![]() ��BC��3��CD��x�����߶�CP�ij������ú�x��ʽ�ӱ�ʾ��
��BC��3��CD��x�����߶�CP�ij������ú�x��ʽ�ӱ�ʾ��
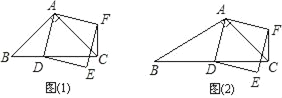
���𰸡���1��CF��BDλ�ù�ϵ�Ǵ�ֱ,���ɼ���������2��AB��ACʱ��CF��BD�Ľ��۳��������ɼ���������3��������
��������
��1���ɡ�ACB=45�㣬AB=AC���á�ABD=��ACB=45�㣻�ɵá�BAC=90�㣬��������ADEF���ɵá�DAF=90�㣬AD=AF����DAF=��DAC+��CAF����BAC=��BAD+��DAC���á�CAF=��BAD����֤��DAB�ա�FAC��SAS�����á�ACF=��ABD=45�㣬�á�BCF=��ACB+��ACF=90�㣮��CF��BD��
��2������A��AG��AC��BC�ڵ�G���ɵó�AC=AG����֤����GAD�ա�CAF�����ԡ�ACF=��AGD=45�㣬��BCF=��ACB+��ACF=90�㣮��CF��BD��
��3����������ADEF�ı�DE����ֱ�����߶�CF����ֱ���ཻ�ڵ�P����AC=4![]() ��BC=3��CD=x�����߶�CP�ij������ǵ�D��λ�ã����������ȥ��𣮢ٵ�D���߶�BC���˶�����֪��BCA=45�㣬�����AQ=CQ=4����DQ=4-x����֤��AQD�ס�DCP���ٸ������������ε�����������⣮�ڵ�D���߶�BC�ӳ������˶�ʱ���ɡ�BCA=45�㣬�����AQ=CQ=4����DQ=4+x����A��AQ��BC��CB�ӳ����ڵ�Q�����AGD�ס�ACF����CF��BD���ɡ�AQD�ס�DCP�����ٸ������������ε�����������⣮
��BC=3��CD=x�����߶�CP�ij������ǵ�D��λ�ã����������ȥ��𣮢ٵ�D���߶�BC���˶�����֪��BCA=45�㣬�����AQ=CQ=4����DQ=4-x����֤��AQD�ס�DCP���ٸ������������ε�����������⣮�ڵ�D���߶�BC�ӳ������˶�ʱ���ɡ�BCA=45�㣬�����AQ=CQ=4����DQ=4+x����A��AQ��BC��CB�ӳ����ڵ�Q�����AGD�ס�ACF����CF��BD���ɡ�AQD�ס�DCP�����ٸ������������ε�����������⣮
��1��CF��BDλ�ù�ϵ�Ǵ�ֱ��
֤�����£�
��AB=AC����ACB=45�㣬
���ABC=45�㣮
��������ADEF��AD=AF��
�ߡ�DAF=��BAC=90�㣬
���DAB=��FAC��
���DAB�ա�FAC��SAS����
���ACF=��ABD��
���BCF=��ACB+��ACF=90�㣮
��CF��BD��
��2��AB��ACʱ��CF��BD�Ľ��۳�����
�����ǣ�
����A��GA��AC��BC�ڵ�G��
�ߡ�ACB=45�㣬
���AGD=45�㣬
��AC=AG��
ͬ����֤����GAD�ա�CAF
���ACF=��AGD=45�㣬��BCF=��ACB+��ACF=90�㣬
��CF��BD��
��3������A��AQ��BC��CB���ӳ����ڵ�Q��
�ٵ�D���߶�BC���˶�ʱ��
�ߡ�BCA=45���������AQ=CQ=4��
��DQ=4��x����AQD�ס�DCP��
��![]() ��
��
��![]() ��
��
��![]() ��
��
�ڵ�D���߶�BC�ӳ������˶�ʱ��
�ߡ�BCA=45�㣬
��AQ=CQ=4��
��DQ=4+x��
��A��AQ��BC��
���Q=��FAD=90�㣬
�ߡ�C��AF=��C��CD=90�㣬��AC��F=��CC��D��
���ADQ=��AFC�䣬
����AQD�ס�AC��F��
��CF��BD��
���AQD�ס�DCP��
��![]() ��
��
��![]() ��
��
��![]() ��
��