题目内容
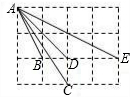 如图所示,在4×3正方形网格中从A点出发的四条线段AB、AC、AD、AE,它的另一个端点B、D、C、E均在格点上(正方形网格的交点).
如图所示,在4×3正方形网格中从A点出发的四条线段AB、AC、AD、AE,它的另一个端点B、D、C、E均在格点上(正方形网格的交点).(1)若每个正方形的边长都是1,分别求出AB、AC、AD、AE长度;(结果可以保留根号)
(2)在AB、AC、AD、AE四条线段中,是否存在三长线段,它们能构成直角三角形?如果存在,请指出是哪三条线段,并说明理由.
分析:(1)在直角三角形中,利用勾股定理可求解各条线段的长度即可;
(2)由勾股定理逆定理可知,三角形两边的平方和等于第三边的平方,则这个三角形为直角三角形,由此可判断是否存在直角三角形.
(2)由勾股定理逆定理可知,三角形两边的平方和等于第三边的平方,则这个三角形为直角三角形,由此可判断是否存在直角三角形.
解答:解:(1)AB=
=
,AC=
=
,AD=
=2
,AE=
=2
(2)AB,AC,AD可构成直角三角形,
∵AD2+AB2=AC2,
由勾股定理逆定理可得,其为一直角三角形.
| 12 + 22 |
| 5 |
| 32 + 22 |
| 13 |
| 22+ 22 |
| 2 |
| 22 + 42 |
| 5 |
(2)AB,AC,AD可构成直角三角形,
∵AD2+AB2=AC2,
由勾股定理逆定理可得,其为一直角三角形.
点评:能够运用勾股定理求解一些简单的计算问题,会运用勾股定理逆定理判断三角形是否为直角三角形.

练习册系列答案
相关题目
 平行四边形?如果存在,求出R点的坐标;如果不存在,请说明理由.
平行四边形?如果存在,求出R点的坐标;如果不存在,请说明理由.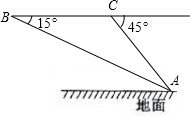 俯角为45°,已知歼10战斗机的飞行速度为600米/秒.求飞机距地面飞行的高度?(结果精确到0.1米)
俯角为45°,已知歼10战斗机的飞行速度为600米/秒.求飞机距地面飞行的高度?(结果精确到0.1米) 影响.试问:
影响.试问: ,过点
,过点 分别作x轴的垂线与反比例函数
分别作x轴的垂线与反比例函数 的图象相交于点
的图象相交于点 ,得直角三角形
,得直角三角形 ,并设其面积分别为
,并设其面积分别为 ,则S5的值为( )。
,则S5的值为( )。
