题目内容
有下列4个命题:①方程x2-(
 +
+ )x+
)x+ =0的根是
=0的根是 和
和 .
.②在△ABC中,∠ACB=90°,CD⊥AB于D.若AD=4,BD=
 ,则CD=3.
,则CD=3.③点P(x,y)的坐标x,y满足x2+y2+2x-2y+2=0,若点P也在y=
 的图象上,则k=-1.
的图象上,则k=-1.④若实数b、c满足1+b+c>0,1-b+c<0,则关于x的方程x2+bx+c=0一定有两个不相等的实数根,且较大的实数根x满足-1<x<1.
上述4个命题中,真命题的序号是 .
【答案】分析:①利用因式分解法解一元二次方程即可;
②利用射影定理直接求出即可;
③利用配方法得出x,y的值,进而得出xy=k的值,即可得出答案;
④根据1+b+c>0,1-b+c<0,即x=1,x=-1时得出y的取值范围,画出图象即可得出较大的实数根的取值范围.
解答: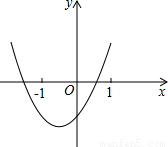 解:①方程x2-(
解:①方程x2-(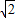 +
+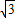 )x+
)x+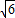 =0的根是
=0的根是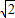 和
和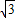 ,此命题正确;
,此命题正确;
②在△ABC中,∠ACB=90°,CD⊥AB于D.若AD=4,BD= ,则CD=3.
,则CD=3.
由题意得出:CD 2=AD×BD,故此命题正确;
③∵点P(x,y)的坐标x,y满足x2+y2+2x-2y+2=0,
∴(x+1)2+(y-1)2=0,
解得:x=-1,y=1,
∴xy=-1,
故点P也在y=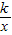 的图象上,则k=-1此命题正确;
的图象上,则k=-1此命题正确;
④∵实数b、c满足1+b+c>0,1-b+c<0,
∴y=x2+bx+c的图象如图所示,
∴关于x的方程x2+bx+c=0一定有两个不相等的实数根,且较大的实数根x满足-1<x<1,故此选项正确.
故答案为:①②③④.
点评:此题主要考查了射影定理即二次函数图象与一元二次方程以及一元二次方程的解法和反比例函数的性质等知识,利用数形结合得出是解题关键.
②利用射影定理直接求出即可;
③利用配方法得出x,y的值,进而得出xy=k的值,即可得出答案;
④根据1+b+c>0,1-b+c<0,即x=1,x=-1时得出y的取值范围,画出图象即可得出较大的实数根的取值范围.
解答:
 解:①方程x2-(
解:①方程x2-(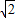 +
+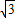 )x+
)x+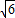 =0的根是
=0的根是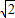 和
和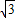 ,此命题正确;
,此命题正确;②在△ABC中,∠ACB=90°,CD⊥AB于D.若AD=4,BD=
 ,则CD=3.
,则CD=3.由题意得出:CD 2=AD×BD,故此命题正确;
③∵点P(x,y)的坐标x,y满足x2+y2+2x-2y+2=0,
∴(x+1)2+(y-1)2=0,
解得:x=-1,y=1,
∴xy=-1,
故点P也在y=
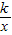 的图象上,则k=-1此命题正确;
的图象上,则k=-1此命题正确;④∵实数b、c满足1+b+c>0,1-b+c<0,
∴y=x2+bx+c的图象如图所示,
∴关于x的方程x2+bx+c=0一定有两个不相等的实数根,且较大的实数根x满足-1<x<1,故此选项正确.
故答案为:①②③④.
点评:此题主要考查了射影定理即二次函数图象与一元二次方程以及一元二次方程的解法和反比例函数的性质等知识,利用数形结合得出是解题关键.

练习册系列答案
相关题目
下列几个命题中正确的个数为 个.
①“掷一枚均匀骰子,朝上点数为负”为必然事件(骰子上各面点数依次为1,2,3,4,5,6).
②5名同学的语文成绩为90,92,92,98,103,则他们平均分为95,众数为92.
③射击运动员甲、乙分别射击10次,算得甲击中环数的方差为4,乙击中环数的方差为16,则这一过程中乙较甲更稳定.
④某部门15名员工个人年创利润统计表如下,其中有一栏被污渍弄脏看不清楚数据,所以对于“该部门员工个人年创利润的中位数为5万元”的说法无法判断对错.
|
个人年创利润/万元 |
10 |
8 |
5 |
3 |
|
员工人数 |
1 |
3 |
|
4 |


